Bài tập, câu hỏi môn học 'Hình thái bờ biển'

Chương 1: Mở đầu

Bài 1.1 Lấy một ví dụ thực tế có thể áp dụng kiến thức môn học hình thái bờ biển.

Bài 1.2 Kể tên các loại bờ biển và nêu đặc điểm chính của từng loại.

Bài 1.3 Liệt kê các quy mô (cỡ) diễn biến bờ biển chính. Khi xây dựng công trình ven biển thì người ta quan tâm đến quy mô thời gian nào?

Bài 1.4 Quỹ bùn cát [CT2018]

Xét Vịnh Diễn Châu (Nghệ An) như trên hình. Theo bạn, các nguồn cấp bùn
cát cho vịnh này có thể đến từ đâu, các nguồn rút bùn cát có thể do đâu?

Chương 2: Sóng, thuỷ triều, nước dâng

Bài 2.1: [DD1992] Người ta quan sát vệ tinh, thấy chiều dài sóng vùng nước sâu là 312 m. Khi đợt sóng này truyền về thềm lục địa gần bờ, quan sát thấy chiều dài sóng chỉ là 200 m. Tính độ sâu nước tại đây.

Bài 2.2 Cho biết chu kì sóng nước sâu bằng 6 s. Tính chiều dài sóng tại vị trí gần bờ, nơi có độ sâu bằng 5 m.

Bài 2.3 Cho biết công thức (chính xác) để tính hệ số nước nông:

$\frac{1}{K_{sh}} = \sqrt{\left( 1 + \frac{2 kh}{\sinh 2kh} \right) \tanh kh}$

a) Dựa vào công thức này, hãy xác định vị trí gần bờ mà K_sh = 1.
b) Giá trị cực tiểu của K_sh bằng bao nhiêu, đạt được ở chỗ nào?

Sau cùng, hãy so sánh với hình vẽ biểu đồ trong quyển giáo trình.

Bài 2.4 [K2000] Hiệu ứng khúc xạ và nước nông.

Cho các đặc trung sóng H₀ = 3,0 m, T = 8,0 s, α₀ = 30°. Hãy tính H và α ở độ sâu nước 10 m.

Bài 2.5 Tính bổ sung các đặc trưng của sóng

Đối với số liệu bài 2.4, hãy tính thêm:

• (mật độ) năng lượng sóng E [J/m²] và năng thông sóng F
  [W/m].
• thành phần ứng suất phát xạ theo hướng truyền sóng tại các vị trí sâu 10 m và 2 m theo công thức: S_ss = (2n – ½)E (hướng truyền sóng vẫn còn xiên một góc α_b ; S_ss khác S_xx).

Bài 2.7 [N2007] Truyền sóng khi có dòng chảy

Trường hợp tổng quát: khi sóng truyền trên nền dòng chảy vận tốc (vec tơ U) thì phương trình phân tán sẽ thay đổi dẫn đến tốc độ truyền sóng khác đi:

$\left( \omega - \overrightarrow{k} \bullet \overrightarrow{U} \right)^{2} = gk \tanh kh$

Theo quy tắc này, bạn nghĩ chiều dài sóng sẽ biến đổi thế nào khi sóng truyền từ biển đến gần một cửa sông?

Bài 2.8 [S2006] Sử dụng các biểu thức tính c, u cho sóng nước nông đồng thời căn cứ vào điều kiện sóng vỡ là vận tốc chất điểm nước tại đỉnh sóng đặt bằng tốc độ truyền sóng, từ đó thiết lập biểu thức chỉ tiêu sóng vỡ. Hãy nhận xét biểu thức này.

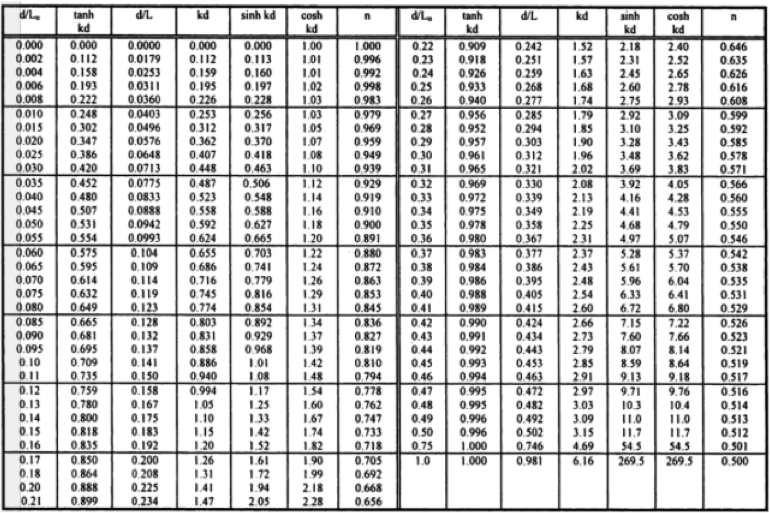
Bài 2.9 [RCF2004] Tính khúc xạ, nước nông, vị trí sóng vỡ.

Sóng nước sâu có chu kì 8,5 s, chiều cao 5 m và có góc 45° so với bờ. Coi rằng các đường đồng mức đáy biển đều thẳng và song song, hãy tính các đặc trưng sóng (chiều cao, tốc độ và góc sóng) cùng với độ sâu nước tại vị trí sóng vỡ.

(Nếu cần, bảng tra sóng của Wiegel được cho ở trên.)

Bài 2.10 [K2000] Với các đặc trưng sóng H_S = 2 m, T_p = 7 s, α₀ = 22° ở độ sâu nước h = 6 m, hãy tính:

a) Các đặc trưng sóng nước sâu: H₀ , T₀ , α₀ ?
b) Các đặc trưng sóng vỡ: H_b , T_b , α_b , h_b , biết rằng độ dốc bãi biển bằng 1:40 và các đường đồng mức được coi như song song với đường bờ.
c) Tính các đặc trưng chuyển động của chất điểm nước tại đáy vị trí sóng
vỡ?

Bài 2.11 [S2006] Sóng có chu kì 7 s ở nước sâu truyền về phía bờ.
Tại độ sâu nào sóng bắt đầu trở thành loại ‘sóng nước nông’? Nếu ở nước sâu, sóng cao 1 m thì liệu con sóng này có vỡ trước khi truyền đến vùng nước nông không? Coi rằng sóng truyền trực diện bờ, không có khúc xạ; và độ dốc bãi biển ven bờ là 1:30.

Bài 2.12 Chiều cao sóng hình thái cho ta biết thông tin gì? Tính chiều cao sóng hình thái cho hướng sóng đông nam (SE) từ số liệu trong slide [9] chương 2.

Bài 2.13 [K2000] Công thức nước dâng cho vùng ven bờ với giả thiết độ sâu biến đổi

Tính nước dâng do bão cho vùng bờ có mặt cắt ngang rộng 10 km, được chia làm 6 đoạn với độ sâu trung bình như trong bảng sau. Bão thổi trực diện với bờ với vận tốc gió U = 20 m/s.

Bài 2.14 [K2000] Một vịnh biển có mặt cắt ngang bãi như bảng dưới đây. Trong một trận bão, gió thổi liên tục trong vòng 4 giờ, trực diện về bãi biển với sức gió 25 m/s. Khí áp tại tâm bão hạ mức 3 kPa. Hãy tính mực nước dâng tại mép nước (coi rằng ở cửa vịnh nước dâng = 0):

Đoạn	1	2	3
Chiều dài (km)	5	5	1.5
Độ sâu TB (m)	7	4	5

Gợi ý: tính phân đoạn để ra độ cao nước dâng S. Sau đó bổ sung nước dâng khí áp = ΔP/ρg.

Bài 2.15 [DD1992] Công thức nước dâng cho vùng ven bờ với giả thiết độ sâu không đổi

Xét thềm lục địa gần bờ có đáy phẳng ngang (độ sâu h = const) và bể rộng ℓ. Hãy lập công thức tính mực nước dâng theo khoảng cách x về phía bờ.

Bài 2.16 [DD2002] Xét vùng thềm lục địa có độ sâu đều h = 5 m, rộng 60 km. Lấy hệ số K_s = 3×10^–6, hãy tính chiều cao nước dâng tại bờ biển ứng với các cấp bão 9, 10, 11, 12.

$\Delta S = h\left\lbrack \sqrt{\frac{2KU^{2}\cos ϕΔx}{gh^{2}} + 1} - 1 \right\rbrack$

Mặt cắt của một bãi biển được liệt kê ở bảng sau

Độ sâu (m)	Khoảng cách (m)
7.31	2750
10.05	4590
13.72	22930
14.62	45860
20.12	48150
23.97	82550
25.6	100890
27.43	107710
36.57	121530
54.86	144460
73.15	181150
91.43	190320

Từ độ sâu 91,43 m trở đi đáy biển dốc sâu rất nhanh và coi như ở chỗ sâu đó không có nước dâng. Khi gió thổi tốc độ 60 knot (30,86 m/s) trực diện vào bờ, hãy tính mực nước dâng tại bờ.

Bài 2.18 [S2006] Khi thủy triều truyền vào cửa sông, độ sâu nước tại vị trí A là 3,7 m. Cũng tại đây, độ lớn triều là 1 m. Thủy triều có dạng bán nhật triều, chu kì 12.4 giờ. Hãy tính vận tốc dòng triều cực đại ở vị trí này.

Tại một vị trí B trong cửa sông nêu trên có độ sâu 5,1 m, hãy ước tính độ lớn triều và vận tốc triều cực đại.

Bài 2.19 Với vịnh triều như trong hình ở quyển giáo trình, khi nào tốc độ dòng triều đạt lớn nhất? Theo em, dòng triều ra và vào vịnh có giống nhau không (về tốc độ dòng chảy và vec tơ hướng dòng chảy)? Hãy thảo luận.

Chương 3: Động lực học ven bờ

Bài 3.1 [S2006] Tại độ sâu nước 5,6 m người ta đo được chiều cao sóng 1,4 m. Nếu sóng này truyền tới bãi biển có độ dốc 1:50 thì bề rộng vùng sóng vỡ sẽ là bao nhiêu? Coi như sóng truyền trực diện vào bờ mà không bị khúc xạ.

Gợi ý: Với câu trên, yêu cầu tính lặp để trước hết xác định H_b. Sau đó, so sánh kết quả H_b này với các công thức kinh nghiệm của Munk (1949); Komar & Gaughan (1972); Kaminsky & Kraus (1993).

Bài 3.2 Sóng nước sâu có chiều cao 1 m, chu kì 5 s, hướng sóng tạo với pháp tuyến đường bờ một góc 30°. Bãi biển có độ dốc 1:100. Chọn chỉ số sóng vỡ γ = 0,6.

Dùng cách tính lặp để các đặc trưng sóng tại điểm sóng vỡ. Sau đó so sánh với công thức thực dụng
$H_{b} \approx \sqrt[5]{\frac{\gamma}{4k_{0}}\mathrm{\cos}^{2}\alpha_{0}H_{0}^{4}}$.
Xác định vị trí đường sóng vỡ (cách bờ bao nhiêu)?

Bài 3.3 Hệ số sóng vỡ γ không phải hằng số!
Tìm hiểu các công thức tính γ ở slide [9] chương 3 và cho biết γ phụ thuộc những yếu tố nào? Tự cho một số giá trị điển hình của các yếu tố trên rồi tính xem γ rơi vào khoảng giá trị nào. Có thể xảy ra γ > 1 không, tại sao?

Bài 3.4 Tính γ kết hợp với kết quả mô hình truyền sóng
Người ta sử dụng chương trình Wadibe để tính truyền sóng dọc theo một mặt cắt ngang bãi biển. Kết quả tính toán được trích cho một đoạn mặt cắt như bảng sau. Kết quả bao gồm khoảng cách ngang từ bờ, cao trình đáy, mực nước, chiều cao và chiều dài sóng. Hãy sử dụng công thức Ruessink để tính γ. Từ đó xét xem trong khoảng 362 < X < 372 (m) có xảy ra sóng vỡ không.

X (m)	Z (m)	η (m)	H (m)	L (m)
362	–9.75	1.08	5.55	128.16
364	–9.85	1.08	5.56	128.66
366	–9.99	1.08	5.57	129.46
368	–10.16	1.08	5.57	130.36
370	–10.34	1.08	5.57	131.26
372	–10.46	1.08	5.58	131.96

Bài 3.5 Để xét sự hình thành sóng vỡ trên mái dốc, ta có thể so sánh trọng lực tác dụng lên chất điểm nước và gia tốc cực đại của chất điểm nước khi theo dòng nước leo lên mái [N2007]. Từ cân bằng hai lực trên hãy lập nên biểu thức Iribarren: ξ = tanβ /$\sqrt{s_{0}}$.

Bài 3.6 Tính chỉ số Iribarren và phân loại sóng vỡ cho các trường hợp sau:

• bãi biển dưới tác dụng của sóng nhẹ mùa hè của H₀ = 0,3 m, T = 4 s, độ dốc đáy tanβ = 0,02
• công trình dưới tác dụng của sóng bão H₀ = 1 m, T = 8 s, độ dốc mái công trình tanβ = 0,25.

Bài 3.7 [K2000] Ghép dạng sóng vỡ (cột bên trái bảng dưới đây) với các điều kiện sóng trên thực tế (cột bên phải):

a) sóng vỡ trên bờ biển vách đá	i) sóng bạc đầu (spilling)
b) sóng lừng trên bãi biển cát	ii) sóng vỡ cuộn (plunging)
c) sóng gió trên bãi biển cát	iii) sóng đổ sập (collapsing)
d) sóng trên bãi biển cuội sỏi	iv) sóng vỗ bờ (surging)

Bài 3.8 Với một giá trị cho trước của γ hãy viết biểu thức nước dâng do sóng và vẽ đường mực nước trung bình nếu coi độ dốc bãi biển sát bờ là 1:10. Từ đó viết ra biểu thức tính nước dâng lớn nhất.

Bài 3.9 [S2006] Xét một con sóng cao 2 m ở vùng nước sâu 2,2 m tại điểm chuẩn bị vỡ. Độ dốc đáy biển vùng sóng vỡ là 0,02. Tính mực nước hạ tại điểm sóng vỡ và độ cao nước dâng tại bờ (mép nước). Cho trước điều kiện sóng nước nông.

Bài 3.10 [DD2002] Nếu đáy biển không phẳng mà có dạng cong lõm (như trên thực tế) và có độ dốc trung bình bằng 0,02 thì các kết quả bài 3.9 sẽ thay đổi như thế nào?

Bài 3.11 [RCF2004] Nước hạ, nước dềnh do sóng & vận tốc dòng chảy dọc bờ
(a) Sóng nước sâu có chu kì 8,5 s và chiều cao 5 m tiến trực diện về bờ. Coi như các đường đồng mức đáy biển song song, hãy ước tính mực nước hạ tại điểm sóng vỡ và chiều cao nước dâng tại đường bờ.
(b) Cũng với sóng đó, nhưng với góc sóng nước sâu là 45°, hãy ước tính vận tốc dòng chảy dọc bờ trung bình trong vùng sóng vỡ. Sử dụng các công thức khác nhau để tính.
(c ) Tính vận tốc quỹ đạo cực đại trong vùng sóng vỡ.

Bài 3.12 Hãy viết phương trình phân bố ngang bờ vận tốc của dòng chảy dọc bờ (V theo X) nếu không xét đến ảnh hưởng của nước dâng. Cho biết độ dốc bãi biển tanβ = 0,01. Các đường đồng mức đáy biển thẳng và song song. Cho các giá trị N = 0,1, C_f = 0,01; γ = 0,7.
Tham số P bằng bao nhiêu? Đối chiếu với Hình 3.12 sách giáo trình, xem dạng đồ thị đã tính được có giống như đồ thị (Longuet-Higgins) trong sách không?
Sau đó trả lời các câu hỏi trong slide [27] chương 2 (trừ câu cuối).

Bài 3.13 Viết phương trình phân bố vận tốc (V theo X) theo số liệu bài 3.12 trong trường hợp có nước dâng.

Bài 3.14 Cho điều kiện sóng ngoài khơi (nước sâu): chiều cao sóng 1 m, chu kì 5 s, hướng sóng tạo với pháp tuyến đường bờ một góc 30°.
Tính giá trị của v₀. Giá trị này có phải vận tốc đo được trong thực tế không?
Sử dụng công thức đã thiết lập trong bài 3.13 (hoặc 3.12) để tính ra các giá trị x (m) và v (m/s) rồi vẽ biểu đồ phân bố vận tốc v ~ x.

Bài 3.15 Cho biểu đồ dạng phân bố (phi thứ nguyên) của dòng ven bờ như hình vẽ. Biết rằng các điều kiện sóng nước sâu là H₀ = 0,95 m, T = 6 s, góc sóng α₀ = 30°. Hãy xác định giá trị vận tốc dòng chảy dọc bờ lớn nhất, v_max (m/s). Vận tốc này xảy ra ở vị trí cách bờ bao xa?

Bài 3.16 Hình dung xem dạng phân bố lưu tốc sẽ ra sao nếu đáy biển phẳng trở nên dốc hơn? Cũng hỏi như vậy nếu thay đáy phẳng là một đáy cong lõm (dạng đáy biển thường gặp ở thực tế)?

Bài 3.17 [DD2002] Giả sử một công trình vuông góc với bờ chặn ngang dòng chảy dọc bở. Theo đó, tại y = 0, V_L = 0. Hãy vẽ một cách định tính sự biến thiên V_L theo trục y (mũi tên đi dọc bờ xa dần công trình).

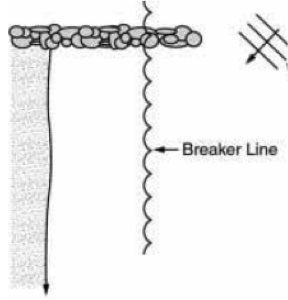
Bài 3.18 [DD2002] Hãy tái lập lại kết quả tính toán vận tốc dòng chảy dọc bờ Giả sử một công trình chắn sóng đến trực diện như hình vẽ. Hãy phác họa dạng dòng chảy dự đoán phía sau công trình, và giải thích.

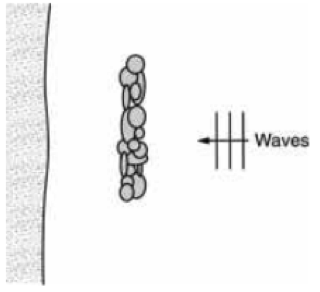
Bài 3.19 Hãy tái lập kết quả tính toán vận tốc dòng chảy dọc bờ như hình 3.18 sách giáo trình cho trường hợp mặt nước dốc thuận chiều dòng chảy, với độ dốc ∂η/∂y = −0,0005.

Chương 4: Vận chuyển bùn cát

Bài 4.1 Slide [3] chương 4: Căn cứ vào thông tin về các chỉ số thống kê của hai mẫu hạt trong bảng, hãy miêu tả sự khác biệt giữa cát bãi biển và trên cồn cát. Theo em điều kiện tự nhiên nào quy định sự khác biệt đó?

Bài 4.2 Với điều kiện dòng chảy ở slide [10] chương 4, hãy xác định đường kính hạt bùn cát được khởi động bởi một dòng chảy có tốc độ trung bình 0,24 m/s.

Bài 4.3 [H2000] Dùng công thức Bijker xác định phân bố (theo phương ngang bờ) lượng vận chuyển bùn cát dọc bờ. [Slide 38].

Gợi ý: Thực hiện tính toán truyền sóng, dòng chảy dọc bờ → chiều cao sóng, lưu tốc tại điểm bất kì theo phương ngang bờ. Chú ý: Bên trong vùng sóng vỡ có thể lấy luôn chiều cao sóng = γ_b × độ sâu nước.

Luyện tập tính công thức Bijker ở ví dụ slide [37].

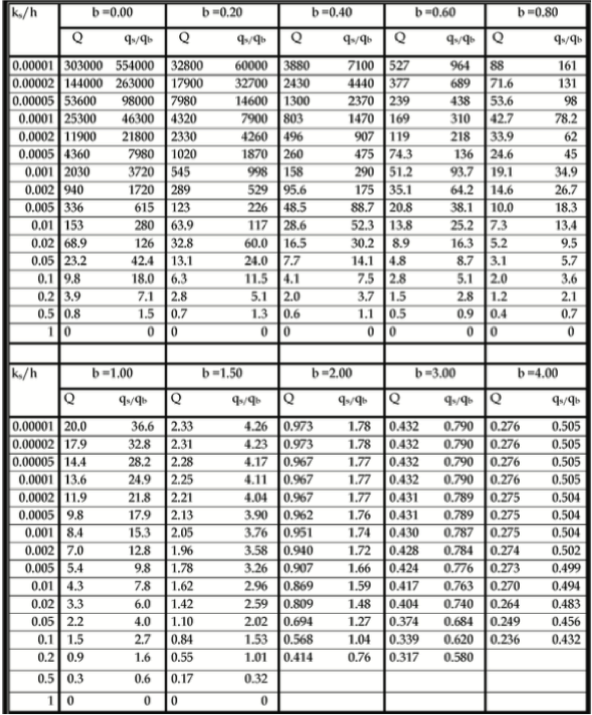
(Ghi chú: trong bảng này đọc b là Z*)

Bài 4.4 Tính lượng VCBC tiềm năng dọc bờ theo công thức CERC

Cho các đặc trưng sóng vỡ: H_b = 1 m (chiều cao sóng ý nghĩa), T_p = 5 s, α_b = 10°; độ dốc bãi biển 1%, đường kính hạt trung vị 200 μm.

a) Tính lưu lượng bùn cát dọc bờ theo công thức CERC. Mỗi năm có bao nhiêu bùn cát di chuyển dọc bờ?
b) Nếu tính theo chiều cao sóng căn quân phương H_rms thì hệ số A_rms nào cho kết quả sát nhất với A = 0,39 tính theo H_s ? Theo Komar (1988) thì A_rms = ?

Bài 4.5 Biến đổi công thức Kamphuis (Queens)

Từ công thức Kamphuis (1990) trong sách giáo trình [32], hãy biến đổi về dạng thu gọn

Q_L = 2,27 H_sb² T_p^1,5(tanβ)^0,75D₅₀^–0,25 (sin2α_b)^0,6   [kg / s]

Tiếp theo hãy quy đổi ra Q_L (m³/năm). { Ghi chú: hệ số trong công thức quy đổi được Schoones và Theron (2000) đề nghị là 63433, sau khi đã nghiên cứu kiểm định với nhiều bộ số liệu thực địa. }

Bài 4.6 Với số liệu bài 4.3, tính lưu lượng VCBC dọc bờ (m³/năm) theo công thức Kamphuis. So sánh với kết quả tính công thức CERC.

Bài 4.7 Phân tích độ nhạy

Giá trị lưu lượng cát Q_L trong công thức Kamphuis phụ thuộc những yếu tố nào? Hãy xét độ nhạy của Q_L theo D₅₀ và theo H_s khi D₅₀ ±10% và H_s ±10%. Nhận xét yếu tố nào ảnh hưởng mạnh hơn trong điều kiện ví dụ đang xét?

Bài 4.8 Cán cân bùn cát (1)

Ở dải bờ biển gấp khúc có 2 đoạn thẳng (xem slide), với một điều kiện sóng thì góc sóng vỡ ở hai đoạn khác nhau → Q_L khác nhau. Giả sử Q_L1 = 0,02 m³/s và Q_L2 = 0,04 m³/s. Đánh giá lượng xói/bồi ở đoạn cong? Nếu chiều dài cong dọc bờ là 1 km và bề rộng vùng sóng vỡ là 150 m thì sau một năm cao trình đáy biển đoạn cong này thay đổi bao nhiêu?

Bài 4.9 Cán cân bùn cát (2)

Dọc bờ biển người ta thấy lượng VCBC (tịnh) ven bờ được biểu diễn như trên hình. Hãy đánh giá xói/bồi?

Bài 4.l0 [DD2002] Bờ biển ban đầu thẳng có một đập mỏ hàn được xây nên. Hướng sóng tới chéo góc.

a) So sánh thể tích bùn cát bồi trước công trình so với thể tích xói phía sau?
b) Kết luận trên còn đúng khi đập mỏ hàn cho dòng cát xuyên qua không?

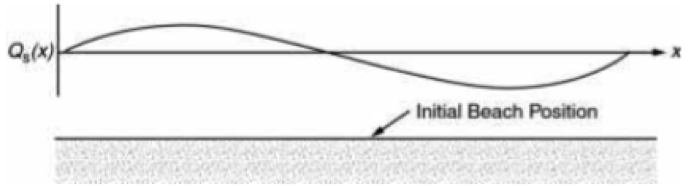
Bài 4.11 [DD2002] Giả sử dọc theo đường bờ thẳng ban đầu có lưu lượng VCBC dọc bờ Q_s (x) phân bố như đồ thị trên hình. Hãy phác hoạ hình dạng đường bờ một thời gian ngắn sau đó.

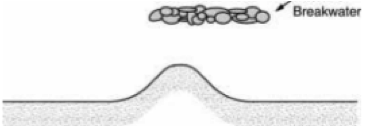
Bài 4.12 [DD2002] Căn cứ vào dạng bồi lắng tại phần khuất của đập chắn sóng xa bờ như hình vẽ bên, hãy phác hoạ hướng sóng chính. Giải thích.

Bài 4.13 Mô hình a-b-c của May và Tanner (1973)

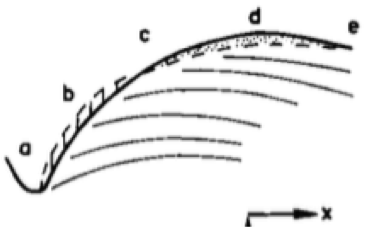
Xét sóng truyền tới vịnh biển như hình vẽ (các đường cong đỉnh sóng được vẽ song song nhau). Với các vị trí a, b, c, d, e dọc bờ như trên hình, hãy tính các giá trị: năng thông sóng dọc bờ (F_L), gra-đien lưu lượng VCBC dọc bờ (∂Q_L/∂x); từ đó giải thích xu hướng thay đổi bờ biển về vị trí mới như đường đứt nét.

Bài 4.13 VCBC thực tế ≠ tiềm năng

Hãy giải thích sự khác biệt giữa lượng VCBC tiềm năng và VCBC thực tế ở các slide [26–27] chương 4.

Bài 4.14 [RCF 2004] Lượng vận chuyển bùn cát dọc bờ theo chế độ sóng

Với số liệu chế độ sóng như trên bảng, hãy ước tính lưu lượng VCBC (tịnh và tổng cộng) dọc bờ một bãi biển tự nhiên có độ dốc đáy 1:100 và đường kính hạt D₅₀ = 0.4 mm.

Hsb (m)	Tp (s)	θb (o)	Tần suất (%)
0.8	4.5	25	5
1.2	5.5	15	10
1.5	6	5	15
1.3	6	-5	12
1.1	5.5	-15	8
0.5	4	-25	5

Ghi chú: Hướng dương và âm là so với pháp tuyến đường bờ.

Lập một bảng tính Excel cho phép tính ra lưu lượng VCBC với số hàng bảng sóng là bất kì.

Chương 5: Diễn biến bờ biển

Bài 5.1 [CT2018] Vùng biển Diễn Châu vào mùa đông có đặc trưng sóng H_s = 0.5 m; T = 3.6 s. Cát bờ biển khá mịn, đường kính D₅₀ = 0,1 mm. Hãy ước tính số Dean (Ω). Bãi biển này thuộc loại gì xét về phương diện năng lượng?

Bài 5.2 [DD2002] Hãy tính và vẽ mặt cắt cân bằng cho các bãi biển cát đường kính hạt 0,2 và 0,4 mm với cùng chiều cao thềm bãi 2,5 m.

Bài 5.3 Với mặt cắt đại biểu bãi biển Tư Hiền năm 1996 hoặc 1997 (slide [8] chương 5) hãy ước tính giá trị hệ số A và từ đó đường kính hạt địa phương.

Bài 5.4 [DD2002] Tại sao trên một mặt cắt ngang bãi biển ta thường thấy có cát thô ở phần gần bờ và cát mịn ở xa bờ?

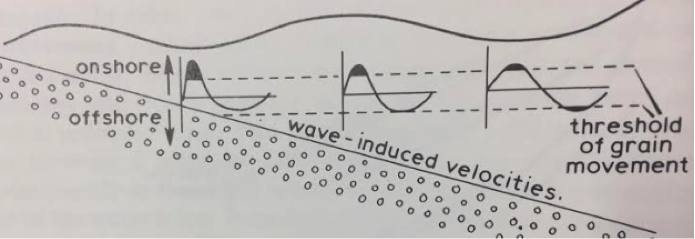
Bài 5.5 Biết rằng khi sóng đều truyền đến gần bờ thì hình dạng sóng càng bất đối xứng (đỉnh nhọn cao, đáy nông rộng), và tốc độ phần tử nước như các đồ thị trên hình vẽ [P1984]. (Ngưỡng tốc độ dòng chảy làm bùn cát dịch chuyển là đường đứt nét.) Hãy chỉ ra xu hướng di chuyển của cát đáy tại các vị trí này trên mặt cắt ngang.

Bài 5.6 [DD2002] Cho mặt cắt ban đầu là phẳng với độ dốc 1:15, hãy tính và so sánh với mặt cắt cân bằng trong điều kiện hạt cát đường kính 0,2 mm, chiều cao sóng vỡ 1,8 m, chu kì 3 s. Độ dốc cân bằng được xác định theo độ sâu sóng vỡ.

Bài 5.7 [DD2002] Xét một mặt cắt lý tưởng ban đầu ở trạng thái cân bằng.

(a) Khi mực nước thay đổi (nâng hoặc hạ), hãy nêu lý do khiến cho mặt cắt được điều chỉnh về một dạng cân bằng mới.
(b) Khi đổ một lượng cát lớn (thô hơn cát hiện có) vào vùng sát bờ thì mặt cắt mới sẽ như thế nào? Phác hoạ.
( c) Tương tự câu (b) nhưng với cát mịn hơn cát hiện có.

Bài 5.8 [DD2002] Giải thích tại sao nếu như hai phía đập mỏ hàn có hiện tượng bồi-xói, thì phần bồi sẽ có bùn cát thô hơn tích tụ?

Bài 5.9 [DD2002] Mặt cắt phức hợp

Một mặt cắt có kích cỡ hạt cát phân bố ở khoảng cách bờ như sau:

• Khoảng cách: 0 → 100 m; D = 0,3 mm
• Khoảng cách: > 100 m; D = 0,15 mm

Tính độ sâu nước tại vị trí cách bờ 250 m.

Bài 5.10 Bãi biển cát có D₅₀ = 0,2 mm. Hãy viết phương trình mặt cắt ngang cân bằng. Khi người ta nuôi bãi với vật liệu cát thô, D’₅₀ = 0,3 mm, thi công đổ trên mái dốc phẳng từ mép thềm bãi xuống đến độ sâu thềm bãi (B + h* = 5 m như hình A) thì thể tích vật liệu cần là bao nhiêu? Sau một thời gian, bãi biển ổn định ở một trạng thái cân bằng mới. Hãy xác định bề rộng của bãi được bồi đắp thêm khi đó (hình B)?

Bài 5.11 Sóng truyền từ ngoài khơi vào bờ trên một mặt cắt ngang bãi biển.

a) Phác hoạ profile vận tốc nước ở vị trí gần bờ, trên đó chỉ ra dòng hồi quy (undertow) và dòng ‘tĩnh’ (streaming) ở sát đáy.
b) Từ công thức tính Q hãy suy ra công thức tính $\overline{V}$ trong slide [21].
c) Tại vị trí có độ sâu 1 m (vùng nước nông), chiều cao sóng 0,4 m, chu kì sóng 4 s, hãy xác định tốc độ trung bình dòng hồi quy và tốc độ dòng tĩnh.

Bài 5.12 Bãi biển có bùn cát đường kính D₅₀ = 0,15 mm. Trong điều kiện sóng lừng có chiều cao sóng H_o = 0,5 m và T = 5 s, hãy tính độ dốc của mặt bãi biển. Từ đó, xác định độ dốc của bề mặt nước dềnh do sóng (wave set-up).

Bài 5.13 [DD2002] Độ sâu giới hạn VCBC

Tính độ sâu giới hạn VCBC cho trường hợp: sóng nước sâu có chiều cao 0,5 m và chu kì 8s và bãi biển cát với cỡ hạt 0,3 mm.

Bài 5.14 Tính độ sâu giới hạn VCBC với số liệu đường kính hạt D₅₀ = 0,2 mm, sóng H_s = (1 ± 0,4) m (giá trị TB ± độ lệch chuẩn), T_s tính theo H_s với giả thiết độ dốc sóng 1:30.

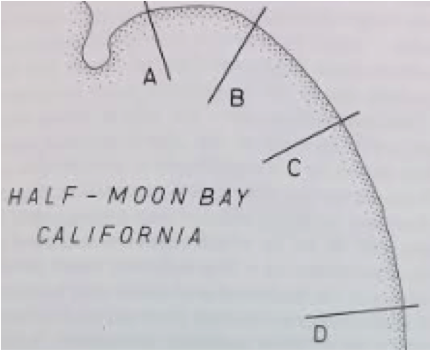
Bài 5.15 Vùng vịnh Halfmoon (Mỹ) có bản đồ đường bờ như hình vẽ [P1984]. Hướng sóng chủ đạo là sóng từ hướng Tây. Hãy dự đoán trong số các mặt cắt A, B, C, D, mặt cắt nào dốc nhất, mặt cắt nào thoải nhất; tại sao?

Bài 5.16 Làm lại ví dụ slide [33] chương 5, với mực nước dâng 0,2 m. Sử dụng công thức Edelman. So sánh với kết quả tính toán bằng công thức Bruun; khi nào hai kết quả này gần bằng nhau? Có thể lý giải điều này dựa trên biểu thức Edelman không?

Bài 5.17 Số liệu mặt cắt như ví dụ slide [33] chương 5, nhưng với “nước biển dâng do biến đổi khí hậu” mỗi năm 1 cm. Tính độ thoái lui đường bờ sau 50 năm.

Bài 5.18 Với số liệu như ví dụ slide [38] hãy dùng công thức Dean [35] để tính thoái lui đường bờ với điều kiện chiều cao sóng vỡ bằng 1 m.

Bài 5.19 Làm ví dụ slide [38-39] chương 5, nhưng bằng cách giải phương trình (*) hoặc (**) [slide 37] bằng máy tính “CASIO”. So sánh với kết quả tính sẵn trong slide (cách tra biểu đồ).

Chương 6: Mô hình hoá diễn biến đường bờ

Bài 6.1 Máng sóng ‘Hà Lan’ ở phòng thí nghiệm trường ĐH Thuỷ lợi có chiều dài 50 m, sâu 1 m. Cần mô phỏng quá trình truyền sóng từ nước sâu vào bờ với điều kiện nguyên hình: độ dốc mặt cắt ngang 2%, sóng nước sâu cao 1 m, chu kì 6 s.

a) Có nên làm mô hình biến dạng không? Nếu có, tỉ lệ chiều cao và tỉ lệ chiều dài bằng bao nhiêu? Nếu không, tỉ lệ chiều dài bằng bao nhiêu?
b) Chiều cao sóng và chu kì sóng nước sâu trong mô hình bằng bao nhiêu?

Bài 6.2 [DD2002] Người ta thí nghiệm mô hình tỉ lệ nhằm xác định dạng mặt cắt bãi biển cân bằng. Ở nguyên hình, đường kính trung vị hạt 0,4 mm, điều kiện sóng gồm chiều cao 1 m và chu kì 4 s. Hãy lập hệ thức tỉ lệ cho các trường hợp sau dựa theo sự tương tự thuỷ lực về số Dean Ω:

(a) Nếu cát dùng trong mô hình có kích cỡ 0,2 mm.
(b) Do kích thước phòng thí nghiệm có hạn nên tỉ lệ dài được chọn bằng 1/25. Nên dùng cát kích cỡ bao nhiêu?

Bài 6.3 Hằng số bờ biển (s_x)
Tại bờ biển sóng vỡ có H_b = 1 m, α_b = 10°. Tính lưu lượng VCBC theo công thức CERC, lấy A = 0,39; γ = 0,7 ; n = 0,4 ; Δ = 1,65.
Tính hằng số bờ biển cho trường hợp này theo hai cách.

Bài 6.4 a) Hãy viết PT cơ bản của diễn biến đường bờ khi lấy hằng số bờ biển ở Bài 6.3; độ sâu giới hạn VCBC bằng 5 m; chiều cao thềm bãi lấy bằng 1 m.
b) Một đập mỏ hàn liền khối được đặt tại vị trí x = 0 trên đường bờ. Viết điều kiện biên của mô hình? Nếu đập này không phải liền khối mà lại cho 20% lượng bùn cát dọc bờ truyền qua nó thì ĐK biên cần được điều chỉnh ntn?

Bài 6.5 Trên đoạn bờ biển thẳng người ta xây dựng một đập mỏ hàn. Coi như đập chắn toàn bộ bùn cát vận chuyển dọc bờ. Sóng tới xiên góc với bờ, φ’ = 10°; lượng VCBC đã tính được bằng 0,032 m/s. Độ sâu hoạt động của bãi biển là B + h* = 12,5 m.

a) Tính bề rộng bãi được bồi tụ tại vị trí cách đập 100 m, sau thời gian 1 tháng.
b) Cũng sau 1 tháng, bề rộng bãi bồi lớn nhất tại đập (x = 0) là bao nhiêu? Thể tích bùn cát bồi tụ bằng bao nhiêu?
c) Tính thời gian cần thiết để bề rộng bãi bồi cực đại đạt 50 m.

Bài 6.6 Hãy lý giải tại sao, trong thời gian không lâu sau khi xây đập, tiếp tuyến của đường bờ tại điểm sát đập có phương vuông góc với hướng truyền sóng? Sau một thời gian dài, khi bùn cát đã vượt qua đầu đập thì tiếp tuyến của đường bờ tại điểm sát đập còn vuông góc với phương vuông góc với hướng truyền sóng không? Hãy vẽ định tính hình dạng đường bờ trong trường hợp thứ hai này?

Bài 6.7 Bờ biển Hải Hậu (Nam Định) chạy thẳng theo hướng Đông Bắc – Tây Nam. Dưới tác động của sóng trong gió mùa đông bắc, dòng VCBC dọc bờ cũng theo hướng nêu trên.

Năm 2014 người ta thi công xây dựng một đập jetty ngang bờ chặn được toàn bộ lượng bùn cát ven bờ. Bạn tìm được một ảnh vệ tinh 2016 chụp khu vực nghiên cứu và nhận thấy mép đường bờ rõ ràng đã lấn ra biển, và đo được khoảng cách bồi lấn này.

Hãy vẽ và thảo luận xem:
a) Có thể ước tính được lưu lượng VCBC dọc bờ không?
b) Khi đã biết mặt cắt ngang bãi biển, có thể ước tính được đặc trưng sóng tại bờ biển không?
Trong từng câu trên, nếu không thì cần thêm thông tin gì nữa?

Bài 6.8 Xét bờ biển ở Bài 6.3. Coi đường bờ ban đầu là thẳng. Coi như sóng đến vuông góc bờ, H_b = 1 m. Người ta thực hiện nuôi bãi với hình dạng mặt bằng là hình chữ nhật với kích thước: dài 500 m dọc bờ, rộng 50 m ngang bờ.

a) Tính hệ số khuếch tán đường bờ.
b) Tính bề rộng tối đa của bãi sau thời gian 1 tháng từ khi nuôi bãi.
c) Tính bề rộng bãi tại một vị trí trong khu vực nuôi bãi, cách mép hình chữ nhật là 100 m.

Bài 6.9 Giả sử vẫn bờ biển được nuôi bãi theo quy cách ở bài 6.8, nhưng sau khi thi công thì sóng thực tế khác với giá trị thiết kế. Người ta quan sát được sau 1 tháng, bề rộng tối đa của bãi còn là 40 m. Ước tính H_b thực tế?

Bài 6.10 [DD2002] Trong dự án nuôi bãi nhân tạo ở Dubai, cát được bơm vào một điểm ở bờ với lưu lượng không đổi. Coi như chiều cao sóng vỡ không đổi. Người ta quan sát thấy đường bờ tiến được 100 m sau 1 năm. Sẽ cần bao nhiêu năm để đường bờ tiến được 250 m so với ban đầu?

Bài 6.11 Hằng năm, sông Thu Bồn đưa lượng phù sa 6×10⁶ m³ ra Cửa Đại. Nghiên cứu [DTMVB2016] cho thấy tại cửa sông chiều cao thềm bãi là 2 m và độ sâu giới hạn VCBC là 6 m; hệ số khuếch tán đường bờ là 125 m²/ngày. Coi như tại một thời điểm trong quá khứ bờ biển này là thẳng. Hỏi từ sau đó 20 năm, bờ biển cửa sông châu thổ này lấn ra biển được bao
nhiêu mét?

Bài 6.12 Phương trình Exner [178] – biến đổi hình thái trên mặt bằng
Sự VCBC ở một vùng cửa sông rất phức tạp. Giả sử tại đây, lưu lượng VCBC đơn vị theo hai hướng x, y được cho bởi: S_x = 0,3 sin(0,15x)exp(–0,6t) và S_y = 0,1 cos(0,12y) exp(–0,4t). Biết n = 0,4, hãy ước tính bề dày lớp bùn cát được bồi tụ (hoặc xói) sau t = 30 ngày, tại vị trí x = 2 m và y = 3 m.

Chương 7: Các giải pháp ổn định đường bờ

Bài 7.1 [DD2002] Xói lở đang xảy ra ở một bờ biển nơi sóng đến trực diện với bờ. Thành phố B được cân nhắc xây dựng đập phá sóng xa bờ để giảm xói.

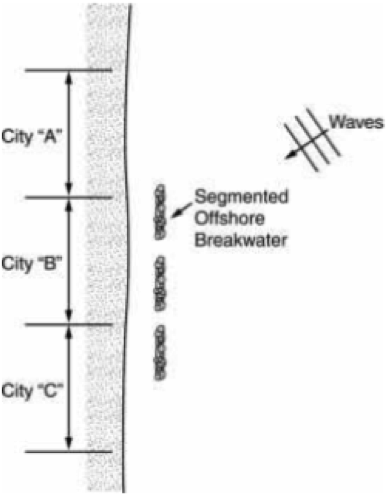
(a) Bạn được các thành phố A và C nhờ tư vấn những tác động xấu (nếu có) của những đập này. Hãy nêu những giả thiết cơ bản của bài toán.
(b) Nên tổ chức dự án quan trắc kiểu gì để ghi lại ảnh hưởng của hệ thống đập đến các TP A& C?
( c) Các đặc tính nào của những đập phá sóng này sẽ chi phối những hiệu ứng xấu nêu trên?

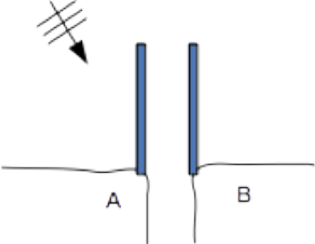
Bài 7.2 Tại một cửa sông, để chống bồi lấp luồng tàu, người ta xây dựng cặp jetty vươn xa khỏi bờ. Coi như jetty chặn toàn bộ lượng bùn cát dọc bờ, hãy phác họa hình dạng đường bờ trong tương lai.
Nếu tại B, người ta gia cố kè cứng thì diễn biến đường bờ sẽ ra sao?

Bài 7.3 Đối với cửa sông ở Bài 6.11, giả sử ở thượng lưu có xây dựng đập thuỷ điện, khiến cho lưu lượng bùn cát hằng năm giảm đi một nửa. Khi đó đường bờ châu thổ tương lai sẽ phát triển như thế nào?

Bài 7.4 Lập một bảng đánh giá độ phù hợp của các giải pháp công trình bảo vệ/ổn định bờ đã học đối với các trường hợp: sóng trực diện bờ, sóng xiên góc, bờ biển dốc/thoải, có cửa sông cấp bùn cát.

Bài 7.5 Cho một ví dụ trong đó sử dụng kết hợp các loại công trình bảo vệ bờ; nêu công dụng của từng loại kết cấu trong hệ thống công trình đó.

Bài 7.6 Khi nào giải pháp ‘thoái lui’ có thể được áp dụng trong điều kiện Việt Nam? Thảo luận.

Tài liệu tham khảo

[DD1992] Dean R.G., Dalrymple R.A. 1992. Water Wave Mechanics for Engineers and Scientists. World Scientific.

[DD2002] Dean R.G., Dalrymple R.A. 2002. Coastal Processes: with Engineering Applications. Cambridge.

[DTMVB2016] Duy D.V., Tanaka H., Mitobe Y., Viet N.T., Binh L.T. 2016. Analysis of erosion and accretion waves on Cua Dai Beach in Central Vietnam. Conference Paper.

[H2000] Coastal Morphology Lecture Notes, IHE-Delft.

[K2000] Kamphuis J.W. 2000. Introduction to Coastal Engineering and Management. World Scientific.

[N2007] Nielsen P. 2007. Coastal and Estuarine Processes. World Scientific.

[P1984] Pethick J. 1984. Introduction to Coastal Geomorphology. Hodder Arnold.

[RCF2004] Reeve D., Chadwick A., Fleming C. 2004. Coastal Engineering: Processes, Theory and Design Practice. Spon Press.

[S2006] Sorensen R.M. 2006. Basic Coastal Engineering, 3^rd edition. Springer.

Biên tập: GV Nguyễn Quang Chiến, 2018