Bài giảng Phương pháp số trong Mô phỏng thuỷ động lực
Bộ môn Quản lý tổng hợp vùng ven biển: Tầng 3 nhà C1
Trường Đại học thủy lợi. Số 175 Tây Sơn, Đống Đa, Hà Nội
Biên soạn: GV Nguyễn Quang Chiến
Phụ trách môn học: Bộ môn Quản lý tổng hợp vùng ven biển
Phiên bản điện tử soạn trên StackEdit.
Mục lục
Lời nói đầu
Phương pháp số đã trở nên phổ dụng để giải quyết những bài toán kĩ thuật hiện đại. Trong lĩnh vực kĩ thuật biển, yêu cầu giải những bài toán phi tuyến phức tạp với nhiều số liệu, do đó càng cần có những phương pháp số hiệu quả. Một ứng dụng cơ bản của phương pháp số là mô phỏng quá trình truyền sóng từ ngoài khơi vào bờ; vốn rất quan trọng để đánh giá mức độ ổn định của bờ biển và hiệu quả của những công trình bảo vệ bờ. Một khía cạnh quan trọng khác là động lực bờ biển vốn có tương tác giữa sóng và dòng chảy. Khi đó phương pháp số sẽ được dùng để giải các phương trình vi phân phi tuyến, cho kết quả về trường sóng, trường dòng chảy trong vùng bờ biển ứng với các điều kiện biên, các ngoại lực khác nhau tác động đến vùng bờ. Một số khía cạnh mô hình hoá sử dụng phương pháp phần tử hữu hạn (một phương pháp số điển hình) cũng được đề cập trong cuốn này.
Tập bài giảng này trình bày cơ sở chung cho phương pháp số và đưa ra một số ví dụ liên hệ trực tiếp với chuyên ngành. Bài giảng phù hợp với môn 2 tín chỉ cho những học viên cao học hoặc sinh viên năm cuối học môn tự chọn. Bài giảng được trình bày cô đọng và người học cần phải chuẩn bị laptop để thực hành, kiểm tra lại nội dung lý thuyết. Hãy xem phần phụ lục.
Khái niệm cơ bản
Phương pháp số có thể xem như là một loạt những bước tính toán hữu ích trong việc xấp xỉ một bài toán. Phương pháp số thường gắn với máy vi tính, tuy vậy máy tính chỉ là một công cụ để thực hiện phương pháp số mà thôi.
Phương pháp số khác với thuật toán ở chỗ: thuật toán cụ thể hơn cho bài toán cụ thể, phương pháp số có thể áp dụng cho một nhóm bài toán. Chẳng hạn, ta có phương pháp số Newton–Raphson để tìm nghiệm của hàm bất kì, còn phương pháp số được triển khai cho một hàm cụ thể, chẳng hạn tìm nghiệm của hàm .
Mặc dù có nhiều phương pháp số khác nhau nhưng tựu chung lại đều tuân theo một số ý tưởng nhất định.
- Kĩ thuật tiếp tuyến: phép xấp xỉ dựa trên khai triển Taylor, cách này thường dùng để xấp xỉ nghiệm.
- Kĩ thuật cát tuyến: phép xấp xỉ này để bổ sung cho kĩ thuật tiếp tuyến, có thể dùng để tính đạo hàm, tính tích phân (như quy tắc hình thang).
- Phép đệ quy: đây là công cụ mạnh để giải quyết bài toán, một khi đệ quy được xây dựng phù hợp. Các ngôn ngữ lập trình hiện đại đều hỗ trợ tốt về tính năng này.
- Tạo số ngẫu nhiên: Việc tạo số ngẫu nhiên bằng máy tính là công cụ quan trọng để giải những bài toán mô phỏng.
Sai số (tuyệt đối) của một đại lượng được cho bởi: , trong đó là giá trị thực của đại lượng còn là giá trị xấp xỉ của đại lượng đó. Sai số tương đối () được cho bởi
Bài tập.[@Dahlquist1974] Cho thấy rằng sai số tuyệt đối trong loga tự nhiên của đại lượng thì gần bằng sai số tương đối của chính đại lượng .
Các sai số có thể phạm phải bao gồm:
- Sai số máy – do các số thực chỉ được biểu diễn bởi những chữ số thập phân hữu hạn, sẽ xảy ra hiện tượng cắt bỏ hoặc làm tròn số.
- Sai số mô hình toán – do các phương trình toán học vẫn chưa diễn tả sát thực hiện tượng.
- Sai số thuật toán để giải mô hình – có thể phát sinh từ quá trình rời rạc hoá miền tính toán bằng các lưới tính.
- Sai số bởi vòng lặp hữu hạn – trong một số bài toán, nghiệm chỉ đạt được ở trạng thái ổn định; điều này đòi hỏi số vòng lặp tính là vô hạn.
- Sai số từ số liệu vào – đặc biệt với những thuật toán rất nhạy với số liệu vào.
- Sai số lan truyền – những sai số trong vòng lặp trước sẽ tích tụ sang vòng lặp sau, đặc biệt đúng với các bài toán phương trình vi phân.
- Sai số từ phía người lập trình.
Bài tập. Lập chương trình dùng phương pháp lặp để giải phương trình phân tán sóng, tìm ra . Đánh giá sự thay đổi giá trị tính toán qua các lần lặp.
Phương trình vi phân thường
Một phần quan trọng của phương pháp số áp dụng trong kĩ thuật (và kĩ thuật bờ biển) nói riêng là giải các phương trình vi phân. PT vi phân là một hệ thức giữa các đạo hàm khác nhau của một hàm chứa một hay nhiều biến. Trong ngành kĩ thuật biển, các biến này có thể là mực nước, độ sâu nước, vận tốc dòng chảy, hoặc năng lượng sóng. Các quá trình vật lý diễn ra có thể được biểu diễn bằng PT vi phân. Khác với phương trình đại số (giá trị của ẩn là con số), trong phương trình vi phân nghiệm là một hàm diễn tả động thái của đại lượng theo các biến độc lập (vốn là thời gian và không gian ()). Các PVR phi tuyến xuất hiện trong tuyệt đại đa số bài toán thuỷ động lực học. Tuy vậy, các thuật giải PVR nói chung đều dựa vào những thuật giải phương trình vi phân thường (PVT), cho nên ta sẽ xét đến PVR sau.
Lý thuyết toán về PVT chia chúng thành nhiều loại, tuy vậy trong môn phương pháp số không xét kĩ như vậy. Đầu tiên, có thể nhận thấy rằng các phương trình bậc cao đều có thể giảm về hệ các phương trình bậc thấp, thông qua việc đặt ẩn phụ. Các phương pháp giải (số trị) cho hệ phương trình cũng không khác gì với từng phương trình một [@Ferziger1981]. Phương trình phi tuyến và tuyến tính không khác nhiều về cách giải, miễn là các phương trình được viết dưới dạng tách riêng đạo hàm cấp cao nhất, Chỉ có điều PT phi tuyến phải thực hiện tính toán “nặng” hơn. Tuy nhiên bài toán biên và bài toán giá trị đầu khác biệt rõ. Trong bài toán điều kiện đầu, có một điểm khởi đầu mà ta có thể giải ra các lớp nghiệm kế tiếp theo chiều tăng của biến độc lập. Còn với bài toán giá trị biên điều này không được và sẽ khó giải hơn. Một số phương pháp giải bài toán điều kiện biên thì dựa trên phương pháp giải điều kiện đầu, bởi vậy ta sẽ tìm hiểu bài toán điều kiện đầu trước.
Vi phân số trị
Vi phân số trị được thực hiện với một số hữu hạn các điểm (khác với vi phân hàm liên tục trong giải tích). Ta giả thiết rằng các số liệu là những giá trị đúng của một hàm trơn qua điểm số liệu này; và chỉ phải tính đạo hàm tại những điểm số liệu mà thôi.
Công thức xấp xỉ vi phân có thể được thiết lập bằng cách dùng chuỗi Fourier. Thật vậy, với hàm có thể viết:
Từ PT (taylor1), chuyển vế ta được:
Để cho tiện, ta sẽ sử dụng cách kí hiệu như sau: Các điểm nút lưới tính toán sẽ có kí hiệu chỉ số dưới cho không gian , và chỉ số trên cho thời gian: . Đôi khi, ta cần sử dụng các điểm “phụ”, chẳng hạn ở chính giữa và . Để cho gọn, ta kí hiệu, . Tương tự, .
Công thức sai phân tiến có thể viết thành: . Đây là công thức sai phân tiến, có độ chính xác cấp 1 theo . Cũng chính PT (forward-diff) là cơ sở của phương pháp Euler (mục 2.3).
Bài tập. Bằng cách kết hợp các phương trình khai triển Taylor, hãy thiết lập các công thức sai phân lùi và sai phân trung tâm. Công thức sai phân trung tâm có độ chính xác cấp mấy?
Bài tập. Rút ra công thức sai phân . (Gợi ý: Khai triển Taylor cho để làm xuất hiện các đạo hàm của .) Độ chính xác của công thức sai phân này là cấp mấy?
Thống nhất, ổn định, và hội tụ
Đây là ba khái niệm đặc trưng cho chất lượng của nghiệm số trị khi khoảng cách giữa các điểm tính toán dần đến 0. Trước khi xét tính thống nhất, ta xét khái niệm sai số cắt cụt (truncation error, TE). Đó là phần chênh lệch giữa nghiệm trơn của bài toán liên tục và nghiệm xấp xỉ rời rạc. Chẳng hạn, với công thức sai phân tiến:
Bài tập. Viết biểu thức sai số cắt cụt cho phương pháp sai phân lùi. Cho thấy rằng mặc dù hai phương pháp này có cùng độ chính xác cấp 1 nhưng các sai số cắt cụt là khác nhau.
Thống nhất (consistency). Một sơ đồ sai phân được gọi là thống nhất nếu nó đảm bảo sai số cắt cụt khi bước tính toán . Tính thống nhất đảm bảo cho sơ đồ sai phân thực sự biểu diễn được PVR.
Ổn định. Một sơ đồ được gọi là ổn định nếu giá trị sai số của đại lượng không bị khuếch đại trong mọi giai đoạn tính toán. Một ví dụ tính toán độ ổn định sẽ được minh hoạ với phương pháp Euler trong mục 2.3.
Hội tụ. Sơ đồ sai phân hội thụ nếu phương trình sai phân đủ sát với nghiệm thực của PVR. Hội tụ là điều kiện mạnh hơn thống nhất (hội tụ = thống nhất + ổn định), tuy nhiên trong thực tế khi thiết lập các sơ đồ sai phân, nói chung hội tụ và thống nhất là đồng nghĩa nhau; khi càng chia nhỏ bước thời gian và bước không gian, nghiệm số trị sẽ hội tụ về nghiệm thực với một sai số cắt cụt hữu hạn.
Ta có thể thiết lập công thức sai phân bằng cách “trực giác” như đạo hàm bậc nhất bằng hiệu giá trị chia khoảng cách, và trong nhiều trường hợp, cách này vẫn đảm bảo tính thống nhất. Chẳng hạn, Chapra [@Chapra1997] đã dùng cách đơn giản để xây dựng công thức đạo hàm bậc hai:
; kết quả thu được giống như thực hiện khai triển Taylor.
Tuy nhiên, không thể lạm dụng cách này để sai phân hoá những phương trình phức tạp. Trong mọi trường hợp, khai triển chuỗi Taylor là cần thiết để kiểm tra xem sai số tiệm cận 0 khi . Xét ví dụ sau đây [@Ramshaw2011]:
Ví dụ. Xét trường hợp miền tính gồm các điểm . Tại phía trái, biên vật lý nằm ở vị trí , trung điểm giữa . Cần xác định giá trị đạo hàm tại điểm . Nếu biên vật lý đặt tại thì ta đã có thể viết , với độ chính xác cấp hai. Nhưng bây giờ phải biến đổi công thức này để tận dụng giá trị . Dường như có thể dễ dàng sử dụng thông tin: là trung điểm vì vậy . Từ đó: . Tuy nhiên, cách này dẫn đến sự không hội tụ! Thật vậy, khai triển chuỗi Taylor quanh điểm cho ta: Nhân đôi hai vế PT dưới sau đó cộng PT trên để triệt tiêu số hạng đạo hàm bậc nhất ta được: . Vậy nếu sử dụng cách khai triển như (*) thì sẽ xấp xỉ được đạo hàm bậc hai, mà thật ra: , tức là chưa xấp xỉ được giá trị đúng của đạo hàm. Tuy vậy, vẫn có thể xấp xỉ được đạo hàm với độ chính xác cấp 1. (Hãy nhân PT trên gần nhất với 4/3, bạn đọc tự thực hiện như một bài tập.)
Bài toán điều kiện đầu trong PVT
Bài toán này có ý nghĩa dự báo. Cho phương trình vi phân với điều kiện đầu cho trước. Một công thức xấp xỉ sai phân đơn giản là: , từ đó cho phép ta dự đoán . Đây là phương pháp Euler tiến.
Lập chương trình tính toán giá trị hàm theo biến ; cho điều kiện đầu và hàm . Quan sát động thái của kết quả dự tính khi thay đổi. Khi giảm , đến một lúc nào đó nghiệm sẽ đột ngột nhảy vọt đến giá trị cực lớn/nhỏ. Ghi lại giá trị này. Ta nói phép sai phân đã mất ổn định (xem đoạn giải thích tiếp theo).
Bây giờ hãy xét sơ đồ sai phân sai phân Euler “lùi”: . Cả hai phương pháp Euler tiến và lùi đều có độ chính xác cấp 1, song chúng khác nhau về độ ổn định. Để đơn giản, hãy xét bài toán: trong đó là hằng số. Phương trình này có nghiệm giải tích trong đó là điều kiện đầu.
Để tính toán ổn định, ta dựa theo hệ số khuếch đại, G = . Với phương pháp Euler tiến, G = . Để đảm bảo điều kiện ổn định, phải có .
Bài tập. Hãy xác định điều kiện ổn định cho phương pháp Euler lùi.
Để cải thiện phương pháp Euler, trước hết ta thấy rằng giá trị đạo hàm tại điểm đầu () hay điểm cuối () đều có thể không biểu diễn tốt độ dốc của đồ thị hàm số . Từ đó, có hai nhóm kĩ thuật cải thiện sau:
- Dự đoán - hiệu chỉnh. Một phiên bản đơn giản của kĩ thuật này là phương pháp “hình thang”, với độ dốc lấy bằng trung bình hai độ dốc đầu và cuối đoạn. Tại bước 1, tính được giá trị dự đoán , giống như Euler tiến, nhưng giá trị này được dùng tiếp. Bước 2, chỉnh lại giá trị vừa dự đoán .
- Trung điểm. .
Hãy lập chương trình tính theo phương pháp Euler tiến, và hai kĩ thuật cải thiện nêu trên. Lưu ý rằng, trong những cách này sẽ cần có giá trị tính trước, khác với phương pháp Euler tiến.
Bài toán điều kiện biên trong PVT
Xét PVT biểu diễn bài toán điều kiện biên sau: trên miền với các điều kiện biên tại (ĐK biên dạng Dirichlet) và tại (ĐK biên dạng Robin). Với những PT dạng đơn giản, đạo hàm phân li được, có thể giải bằng phương pháp bắn (shooting): Bắt đầu với ĐK biên phía , giải PT theo chiều tăng dần (tương tự như ta đã làm với ). Giải đến kết quả tại thì so sánh với điều kiện biên tại đó và điều chỉnh lại nghiệm sao cho giá trị thu được tại đúng bằng ĐK biên [@Chapra2005].
Tuy vậy, các PT vi phân thường phức tạp và nên được giải bằng cách sai phân. Theo đó có thể viết (công thức sai phân từ bài [fwd-bak-ctr]):
Từ đó, có thể viết lại dưới dạng phương trình đại số tuyến tính: Và hình thành nên ma trận gồm ẩn () với phương trình. Để có thể giải được, cần bổ sung hai điều kiện biên đã nêu ở đề bài. Do vậy, PT đầu trong hệ trở thành còn PT cuối trở thành .
Đặt và để tiện biểu diễn các PT “giữa”, ta có hệ phương trình ba đường chéo. Ở đây các hệ số bằng 0 thì được bỏ trống.
Mặc dù đã có nhiều thuật toán tốt để giải hệ phương trình đại số tuyến tính nhưng với các ma trận thưa như hệ 3 đường chéo thì có kĩ thuật giải riêng, như thuật toán Thomas.
Bài tập. Lập hàm trong Julia, nhận các tham số là các vec-tơ (đều có độ dài ) là A, B, C, R và giải ra vec-tơ X. Thuật toán Thomas được liệt kê dưới dạng mã lệnh dưới đây. Sau đó, lập chương trình để giải bài toán vi phân trên với .
for i = 2:N
A[i] /= B[i]
B[i] -= A[i]*C[i-1]
end
for i = 2:N
R[i] -= A[i]*R[i-1]
end
X[N] = R[N] / B[n]
for i = N-1:-1:1
X[i] = (R[i] - C[i] * X[i+1]) / B[i]
end
Vấn đề sai phân tại biên. Ta đã thấy tại các vị trí biên không thể sai phân trung tâm để đạt độ chính xác cấp hai được. Thay vào đó, cần phải xây dựng công thức mới biểu diễn sai phân tại biên mà vẫn giữ được độ chính xác cấp 2. Chẳng hạn, tại biên trái, ta có thể chọn ba điểm 1, 2, 3 để lập sai phân tại biên [@Anderson1995]. Có thể coi một đường cong đi qua ba điểm này với vị trí tương ứng . Có thể rút ra cùng 2 PT: . Hai PT sau này được biến đổi để rút ra: . Mặt khác, ta cần tính ; . Vậy .
Bài tập. Khai triển Taylor để thấy đạo hàm trên được tính với độ chính xác cấp 2.
Lưới điểm không đều
Với mục đích cụ thể, người ta có thể dùng lưới với khoảng chia không đều. Khi đó, kí hiệu . Với lưới điểm không đều, sai phân trung tâm chỉ có độ chính xác cấp 1 như sai phân tiến hoặc lùi.
Bài tập. Làm thế nào để điều chỉnh công thức sai phân chỉ sử dụng giá trị hai điểm và nhưng vẫn đạt được độ chính xác cấp 2?
Đạo hàm trên lưới điểm không đều có thể được tính theo cách đề xuất bởi Chapra và Canale [@Chapra2005]:
Ngoài sai phân hữu hạn còn gì nữa?
Ta đã giải PVT bằng cách số trị—tức là xấp xỉ nghiệm của PV—qua việc tính tại nhiều thời điểm cách đều nhau. Trong việc giải PVR có hai vấn đề: biểu diễn nghiệm (hàm) số liên tục dưới dạng một tập hợp các điểm số liệu (véc-tơ), và việc tính đạo hàm tại các điểm đó. Có hai phương châm cơ bản là: nhóm phương pháp điểm lưới và nhóm phương pháp khai triển chuỗi. Ở lời giải Euler, ta sử dụng phương pháp sai phân hữu hạn (FDM) thuộc nhóm phương pháp điểm lưới. Trong sai phân hữu hạn, chỉ có thông tin tại các điểm lưới chứ không có giả thiết gì về giá trị xấp xỉ giữa các nút lưới này.
Một dạng phương pháp quan trọng là thể tích hữu hạn (FVM), trong đó có giả thiết về cấu trúc của nghiệm xấp xỉ giữa các điểm nút lưới này. Trong phương pháp FVM, giá trị tại nút lưới biểu diễn trị trung bình của hàm trên đoạn, hay ô lưới, . FVM rất hợp sử dụng để xấp xỉ các hàm có điểm gián đoạn. Nếu hàm trơn thì hai phương pháp FDM và FVM cho kết quả như nhau [@Durran2010].
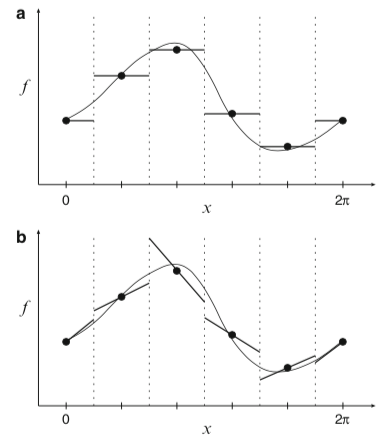
Hình. Xấp xỉ FVM cho một hàm tuần hoàn, dùng đến (a) các hàm bậc thang cho từng đoạn, (b) các hàm tuyến tính cho từng đoạn [@Durran1999].
Về việc tính đạo hàm tại nút lưới, nếu như FDM sử dụng một trong các cách sai phân tiến / lùi / trung tâm, thì FVM quy định giá trị đạo hàm qua cấu trúc được giả sử cho nghiệm xấp xỉ trong các ô tính. Nói riêng, trong FVM, thường tính thông lượng (flux) xuyên qua cạnh các ô tính thay vì đạo hàm; nhưng để tính được các thông lượng này thì phải giả sử cấu trúc nghiệm trong từng ô lưới. Giả sử này không thể chỉ là nội suy tuyến tính giữa các điểm nút lưới; bởi nếu vậy thì giá trị tại nút lưới sẽ không thể bằng trung bình giá trị trong từng ô lưới bao lấy nó được. Phương pháp FVM sẽ được xét đến cùng với các PVR.
Trong nhóm phương pháp khai triển chuỗi, hàm chưa biết được xấp xỉ bởi một tổ hợp tuyến tính từ tập hợp các hàm khai triển liên tục, còn bộ số liệu mô tả hàm xấp xỉ là tập hợp các hệ số khai triển. Các đạo hàm được tính giải tích qua việc vi phân các hàm khai triển. Khi các hàm khai triển này là tập trực giao thì phương pháp được gọi là phương pháp phổ. Một ví dụ là chuỗi Fourier, chẳng hạn xấp xỉ 5 điểm bởi . Nếu các hàm khai triển chỉ khác 0 trong một khu nhỏ của cả miền tính, thì kĩ thuật khai triển chuỗi được gọi là phương pháp phần tử hữu hạn (FEM). Các hàm khai triển khi đó có thể được chọn là hàm tuyến tính từng đoạn. Mỗi hàm nhận giá trị = 1 tại một điểm nút nhất định và = 0 với tất cả điểm nút khác. (Giữa các nút, giá trị của hàm được xác định bằng nội suy.) Với dạng này, FEM thường cho kết quả giống với phương pháp điểm lưới.
Phương trình vi phân riêng
Trong các bài toán thuỷ động lực, ta thường gặp các PVR tuyến tính bậc 2 với ít nhất hai biến độc lập. Chẳng hạn:
-
PT sóng phi tuyến mô tả quá trình diễn biến cuả mặt front shock do tính phi tuyến của sóng, áp dụng trong khí động lực học.
-
PT Burgers mô tả quá trình chuyển tải phi tuyến và khuếch tán, được áp dụng cho các sóng âm, sóng nước. Với có thể áp dụng cho chất lỏng không nhớt, và dạng PT Burgers không nhớt chính là dạng PT sóng phi tuyến nêu trên.
-
Hệ phương trình St Venant cho dòng chảy 1 chiều có mặt thoáng. Có hai dạng trình bày phương trình này: dạng bảo toàn trong đó các biến lượng là diện tích mặt cắt, , và lưu lượng, . Dạng không bảo toàn được đề cập dưới đây có các biến lượng độ sâu nước, , và vận tốc dòng chảy, ; dạng này có hình thức đơn giản hơn nhưng nhược điểm là không áp dụng được khi dòng chảy có đột biến, ví dụ nước nhảy. Hệ PT St-Venant còn được gọi là hệ phương trình nước nông, hệ PT sóng dài, và (bằng cách mở rộng ra 2 chiều) được áp dụng cho thuỷ động lực ven bờ như động thái dòng triều và dao động nước trong bể cảng.
-
Hệ phương trình Navier-Stokes cho dòng chảy 3 chiều của chất lỏng nhớt nén được; có thể coi là phương trình tổng quát chi phối động thái của những chất lưu Newton: trong đó các chỉ số thể hiện tổng các số hạng theo các chiều không gian còn là đại lượng được bảo toàn. Tuỳ vào các điều kiện cụ thể mà hệ PT Navier-Stokes được giản hoá để mô tả dòng chảy không nén được, dòng không nhớt, dòng chảy thế, dòng chảy rất chậm (creeping flow, có độ nhớt lớn); và dùng các phép xấp xỉ như Boussinesq và lớp biên.
Phương trình phi thứ nguyên
Một kĩ thuật đôi khi được dùng trong mô phỏng thuỷ động lực là làm phi thứ nguyên phương trình; nhằm mục đích biểu thị độ lớn tương đối giữa các số hạng thành phần trong phương trình, từ đó có thể giúp ta định hướng giải đúng đắn [@Wood1993]. Chẳng hạn, từ phương tình Navier-Stokes 1 chiều cho dòng không nén được: với là áp suất và là độ nhớt động học. Phương trình có thể được phi thứ nguyên hoá bằng đưa vào các đại lượng tham chiếu về chiều dài (), vận tốc (); khi đó ta thiết lập được các biến phi thứ nguyên:
Thay các biến phi thứ nguyên vào PT N-S 1 chiều, sau đó nhân hai vế với ta thu được: Ở đây đã đưa vào số Froude Fr = và số Reynolds Re . Trong dòng chảy tự nhiên, số Re thường lớn (dòng chảy rối) và số hạng đạo hàm bậc hai () thường được bỏ qua. Còn độ lớn của số Fr cho biết trạng thái của dòng chảy là êm, xiết, hay phân giới.
Việc chọn các đại lượng tham chiếu trong các dòng chảy đơn giản thì rất hiển nhiên: được chọn là vận tốc dòng đều, là chiều sâu dòng đều hoặc chiều dài thuỷ vực. Sau khi đã biến đổi phương trình thì hoàn toàn có thể áp dụng sai phân cho phương trình phi thứ nguyên này. Mặc dù vậy, với các dạng dòng chảy phức tạp, có nhiều quá trình vật lý diễn ra dẫn đến số biến phi thứ nguyên tăng lên khiến cho tính toán khó khăn hơn. Bởi vậy, trong các chương trình phần mềm không phải lúc nào cũng áp dụng cách làm này và phương pháp chỉ được nêu ra đây mà thôi.
Phân loại PVR
Với hai biến , và đại lượng là hàm (phụ thuộc ) cần xác định, dạng tổng quát của PVR như sau:
trong đó có thể là các hàm của , hoặc cả hai, hoặc chỉ là hằng số. Định thức của PT vi phân bậc hai nêu trên là: .
Tuỳ theo dấu của , PT vi phân (tổng quát) được chia thành:
- PVR elip, nếu với nghiệm trơn, dễ giải;
- PVR hyperbol (), với nghiệm có thể chứa điểm gián đoạn, thường khó giải;
- PVR parabol (), có thể mang đặc tính của cả 2 loại PVR trên.
Mỗi loại PVR nêu trên mô tả một loại hiện tượng vật lý trong thuỷ lực. Dạng elip biểu thị diễn biến ổn định, không phụ thuộc thời gian (như dòng nước ngầm ổn định, các đường backwater trong thuỷ lực kênh hở). Dạng hyperbol biểu thị các quá trình vật lý phuộc thuộc thời gian, có tính bảo toàn (như quá trình chuyển tải / đối lưu), không ổn định và không có xu hướng tiến tới trạng thái ổn định. Cuối cùng, dạng parabol biểu diễn các quá trình mang tính tiêu tán, phụ thuộc vào thời gian (chẳng hạn khuếch tán) vốn hướng đến một trạng thái ổn định.
Khác với PVT, các PVR thường dùng lược đồ bậc thấp hơn. Có hai lý do: thứ nhất sai số do vi phân thời gian không phải là nguồn duy nhất gây sai số đến nghiệm. Thứ hai là để giảm công thực hiện tính toán.
Nghiệm của PVR có thể giải được nếu xác lập đầy đủ điều kiện ban đầu và điều kiện biên. Có ba loại điều kiện biên: Dirichlet (ấn định giá trị tại biên), Neumann (ấn định gradient tại biên) và Robin (loại hỗn hợp).
Sự ảnh hưởng của điều kiện đầu, điều kiện biên đến nghiệm của bài toán được thể hiện như trên Hình characteristics. Trong bài toán PVR hyperbol trong 1 chiều không gian, có 2 đường đặc tính; với bài toán parabol thì 2 đường đặc tính này suy biến thành một; còn bài toán elip thì không có đường đặc tính nào (toàn bộ miền tính đều ảnh hưởng đến nghiệm).
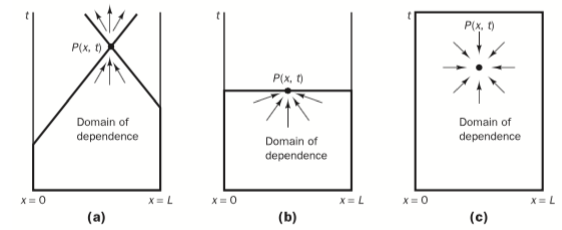
Hình … Các miền ảnh hưởng đến nghiệm trong PT vi phân [@Versteeg2007]: (a) hyperbol, (b) parabol, và ( c ) elip
Một vấn đề quan trọng trong việc giải PVR là sai số. PVR dạng hyperbol dễ mắc sai số nhất vì các điều kiện biên sẽ gây nên sai số truyền đi vào bên trong miền tính.
Phương trình khuếch tán
Phương trình khuếch tán trong không gian 1 chiều có dạng: Đây là phương trình dạng parabol. Hằng số là hệ số khuếch tán. Có thể sai phân hoá theo kiểu FTCS như sau: Từ đó rút ra công thức dự tính giá trị tại thời điểm tương lai:
Bài tập. Bài toán “khuếch tán đường bờ”: Giả sử miền tính toán đuọc chọn là bờ biển dài 1 km; người ta thực hiện nuôi bãi nhân tạo trong phạm vi dọc theo 200 m ở khoảng chính giữa đường bờ trên. Bề rộng của vùng đổ cát là 5 m. Tác động của sóng khiến cho bùn cát bị khuếch tán và sẽ dàn sang hai bên. Cho hệ số khuếch tán đường bờ m/năm, hãy biểu diễn vị trí của đường bờ.
Có thể nhận thấy rằng, trong bài tập trên, không thể chọn nhỏ tuỳ ý vì nghiệm sẽ mất ổn định. Biểu thức ràng buộc giá trị của sẽ được làm sáng tỏ thông qua phép phân tích ổn định. Cũng như trong mục 2.3, chỉ số để đánh giá ổn định là hệ số khuếch đại , song ở đây có khác vì có mặt những giá trị ở các điểm lân cận, và . Để giải quyết điều này, phương pháp Von Neumann được dùng. Coi rằng sai số gắn với là trong đó là số ảo còn là một số sóng của nhiễu động sai số. Khi đó, từ PT [rời rạc hoá] ta có: với lưu ý , có thể rút gọn số hạng chung , và
với , biểu thức được viết thành:
Phép sai phân này chỉ ổn định khi hay . Vì cos(…) < 1 nên luôn đúng. Chỉ cần xét hay . Rõ ràng vì nên .
Phương pháp Von Neumann đã dùng ở trên áp dụng được với các bài toán điều kiện đầu dạng tuần hoàn và hệ số khuếch tán là hằng số. Mặc dù vậy, trường hợp biến đổi trên miền tính thì vẫn có thể dùng phương pháp này để phân tích ổn định cục bộ.
Cũng từ ví dụ về sơ đồ FTCS cho bài toán khuếch tán, có thể thấy rõ rằng một trị số chỉ phụ thuộc vào ba trị số ở bước thời gian trước đó, là và do vậy phụ thuộc vào 5 trị số ở bước trước nữa: . Cứ như vậy, miền ảnh hưởng nghiệm số trị biểu diễn trên mặt phẳng là một tam giác cân (một cách biểu diễn tương tự, nhưng cho bài toán khác, có thể thấy trên Hình [delta-t]). Một điều phi lý của sơ đồ sai phân là lẽ ra mọi điểm cùng lớp thời gian phải có ảnh hưởng đến mới đúng bản chất hiện tượng khuếch tán trong thực tế. Điều này được khắc phục bằng một sờ đồ sai phân ẩn (mục 3.6).
Quá trình giải kiểu “duyệt binh”. Không chỉ có FTCS mà mọi phương pháp khác để giải PT vi phân theo thời gian đều thực hiện kiểu “duyệt binh” (marching). Khi biểu diễn miền tính toán là lưới có trục hoành và trục tung , mỗi đường lưới nằm ngang là tập hợp nghiệm số ở từng lớp thời gian; chúng phải được giải xong (dù giải đồng thời hay lần lượt) trước khi chuyển sang lớp thời gian tiếp theo. Quá trình chuyển động theo hàng này gợi đến hình ảnh duyệt binh, và tương phản với quá trình “căn chỉnh” khi giải PT elip 2 chiều (mục 3.8), khi đó trị số mỗi điểm nút trong hệ phải được liên tục điều chỉnh theo các trị số nút kề bên, sao cho giá trị tổng thể của toàn miền tuân theo PT cơ bản (kiểu Poisson hoặc Laplace).
Phương trình chuyển tải 1 chiều
Phương trình chuyển tải một chiều (1-D convection) rất thông dụng trong các bài toán thuỷ động lực học như một phép kiểm tra chất lượng của các phương pháp sai phân. PT có dạng:
trong đó = const là tốc độ chuyển tải; tuỳ theo dấu của mà hiện tượng chuyển tải theo hoặc ngược chiều dương trục .1
Sơ đồ sai phân FTCS cho PT [1D-conv] là:
Khác với trường hợp PT khuếch tán, dạng sai phân FTCS của PT chuyển tải luôn bất ổn định vô điều kiện, nghĩa là dù thu ngắn bước thời gian đi bao nhiêu nữa, nghiệm số trị vẫn không thể hội tụ.
Bài tập. Bằng phương pháp phân tích ổn định Von Neumann, hãy cho thấy rằng sơ đồ FTCS cho bài toán chuyển tải 1 chiều là bất ổn định không điều kiện (nghĩa là với mọi ). (Gợi ý: một số biến đổi toán học hữu ích: và .)
Để khắc phục nhược điểm của FTCS, người ta đã xây dựng những sơ đồ sai phân tốt hơn để giải PT chuyển tải một chiều:
Sơ đồ Lax không sử dụng giá trị “tại chỗ” để tính sai phân tiến theo thời gian, mà dùng trung bình hai giá trị lân cận, . Trong sơ đồ Lax-Wendroff, số hạng được bổ sung thêm ở vế phải có dáng vẻ của thành phần “khuếch tán”. Việc đưa vào số hạng này để bù cho số hạng bậc hai – số hạng đầu trong sai số cắt cụt với sai phân thời gian ở vế trái. Thật vậy,
Sơ đồ ngược dòng sử dụng sai phân tiến/lùi trong không gian và chỉ có độ chính xác bậc nhất, nhưng một chi tiết quan trọng của kĩ thuật ngược dòng là một điểm nào đó trong đoạn được sai phân sẽ mang thông tin với tốc độ truyền sóng đến điểm cần dự tính trong tương lai.
Bài tập. Sự lan truyền hình dạng sóng. Lập chương trình thực hiện sai phân FTCS với bài toán chuyển tải 1 chiều có trên miền dài . Điều kiện đầu là hàm “mũ phù thủy”: Giảm nhỏ để thấy rằng không thể triệt tiêu được những nhiễu động. Sửa đổi sơ đồ FTCS bằng một trong các phương pháp cải thiện (Lax, Lax-Wendroff, ngược dòng). Sau đó, hãy đổi dấu của và quan sát động thái kết quả.
Các hàm gián đoạn kiểu “bậc” thường được sử dụng để kiểm chứng chất lượng của lược đồ sai phân cho bài toán chuyển tải 1 chiều.
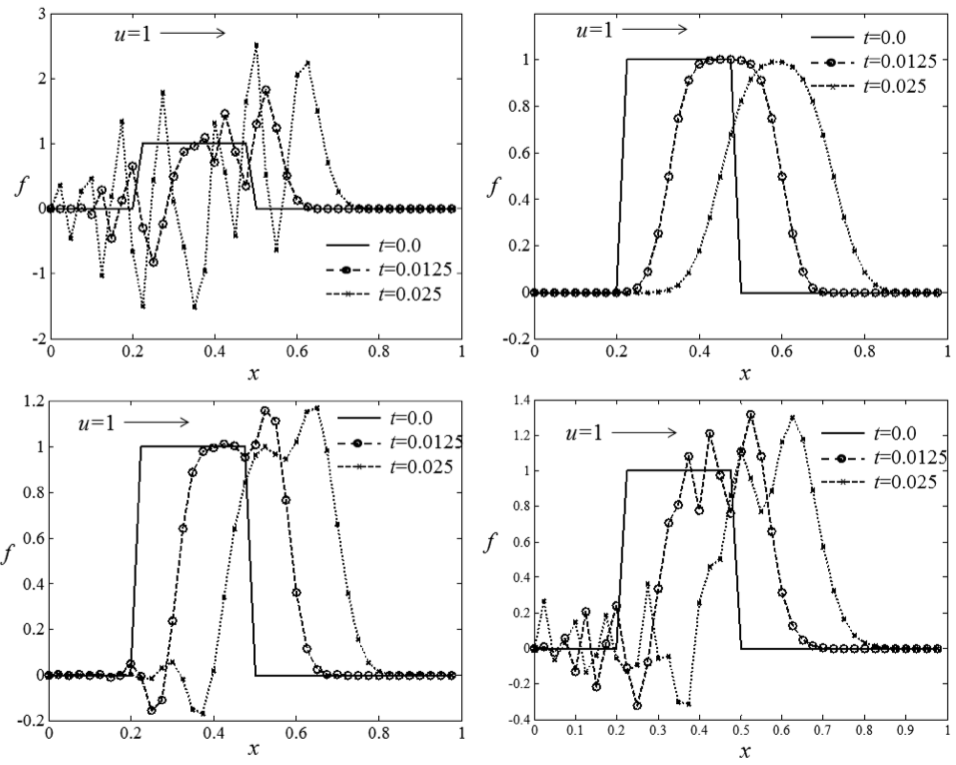
Hình. Nghiệm số trị cho PT chuyển tải ( = 0.5) tính theo các phương pháp khác nhau: FTCS (phía trái trên), ngược dòng bậc nhất (phải trên), Lax–Wendroff (trái dưới) và Crank–Nicolson (phải dưới). [@Watanabe2013]
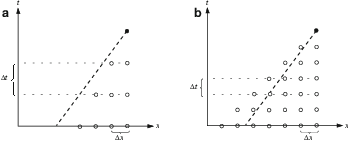
Hình. Ảnh hưởng của độ lớn bước thời gian tới tương quan giữa miền phụ thuộc của sơ đồ ngược dòng (các điểm ) và của PT chuyển tải 1 chiều (đường đứt nét). (a) ổn định, (b) không ổn định.[@Durran2010]
Bài tập. Bằng phương pháp Von Neumann, phân tích ổn định với sơ đồ ngược dòng. Biểu thức của điều kiện ổn định có thể được đưa về dạng . Đại lượng không thứ nguyên vế trái là số Courant.
Bất đẳng thức trong bài trên là điều kiện Courant; với hàm ý tốc độ dòng chảy, , phải nhỏ hơn tốc độ truyền thông tin trên lưới tính, . Cụ thể, như trong hình [delta-t], với cùng tốc độ thì miền ảnh hưởng đến nghiệm số PT sẽ có dạng tam giác tạo bởi đường đứt nét và hình chiếu của nó. Với nhỏ, các điểm nút mà giá trị được dùng cho sai phân che kín hết miền ảnh hưởng.
Miền ảnh hưởng đến nghiệm số trị được biểu diễn dưới dạng một vùng các điểm kề nhau trên lưới tính. Dĩ nhiên lược đồ sai phân hiện sẽ tạo nên vùng ảnh hưởng tam giác có đỉnh nhọn hướng lên. Với lược đồ cho bài toán khuếch tán, miền tam giác cân sẽ trải đều về hai phía trục .
Phương trình chuyển tải-khuếch tán
Đây là dạng kết hợp của hai PVR vừa đề cập đến. Một ví dụ ứng dụng là sự lan truyền chất ô nhiễm dọc theo đoạn sông. Nồng độ chất, , biến đổi theo cả phương dọc sông, , và thời gian, :
Dòng chảy mang chất ô nhiễm đi có tốc độ chuyển tải = const (cỡ 1 m/s). Sự khuếch tán rối làm lan rộng chất ô nhiễm với hệ số khuếch tán = const (cỡ 1 m/s). Tải lượng chất ô nhiễm là với = const phân bố đều trên đoạn sông. Số hạng cuối (không chứa đạo hàm của ), sau khi chuyển vế, được gọi là số hạng nguồn. Cách sai phân số hạng nguồn nằm chính ở trong nội dung của bài toán điều kiện đầu, mục 2.3.
Bài tập. Bài toán dầu thải [@Chapra1997]: Một dòng sông có đặc trưng sau: bề rộng: 60 m, chiều sâu: 1 m, vận tốc dòng chảy trung bình: 2400 m/giờ, hệ số khuếch tán 150000 m/giờ. Giả sử có lượng dầu là 5 kg thải ra tại vị trí 500 m hạ lưu khu dân cư. Hãy viết phương trình sai phân và lập chương trình tính ra phân bố của nồng độ dầu dọc theo sông, cụ thể tại các thời điểm 0.2 giờ, 0.4 giờ, 0.6 giờ sau khi xả thải. Chọn các bước điểm nút lưới và bước thời gian thích hợp. Nghiệm giải tích có dạng
Gợi ý: Dùng điều kiện Pe < 2 (xem thêm mục dưới) để xác định chiều dài đoạn sông phù hợp. Sau đó dùng điều kiện ổn định khuếch tán, để xác định bước thời gian phù hợp. Để xác lập được điều kiện đầu, cần ấn định nồng độ cho 1 đoạn sông đúng chỗ xả thải, (nồng độ ban đầu của các đoạn khác thì bằng 0).
Quan điểm trên về việc coi là chiều dài đoạn thay vì khoảng cách giữa các điểm nút là điều thường gặp trong lĩnh vực mô hình hoá chất lượng nước; một dòng sông được chia thành nhiều “thể tích kiểm soát”, như phương pháp thể tích hữu hạn (FVM) ở mục 4. Ưu điểm của cách làm này là trực quan, có thể căn cứ vào bề rộng sông để phân đoạn sao cho mỗi đoạn có dạng hình lăng trụ ( const), dù phải chấp nhận việc tâm của các thể tích kiểm soát này sẽ không cách đều nhau.
Giải thích điều kiện về số Péclet. Số Péclet trong bài toán chuyển tải-khuếch tán được định nghĩa là Pe = . Nó thể hiện độ mạnh tương đối giữa quá trình chuyển tải và khuếch tán.2 Khi sử dụng phương pháp ngược dòng cho số hạng chuyển tải cùng với sai phân trung tâm cho số hạng khuếch tán, phép ngược dòng chỉ đảm bảo độ chính xác cấp 1 với số hạng lớn nhất trong sai số cắt cụt là (xem lại PT [TE]). Điều đó dẫn đến PT: , nghĩa là hệ số khuếch tán đã tăng thêm một lượng bằng Pe , đây gọi là thành phần khuếch tán giả (false diffusion) hay khuếch tán số trị. Đây cũng là nguyên nhân của biểu hiện nghiệm số trị tính theo phương pháp ngược dòng sẽ bị bẹt đi theo thời gian.
Bài tập. Biến đổi để thu được công thức trên. Muốn giữ cho lượng khuếch tán số trị nhỏ hơn khuếch tán thực thì Pe phải thỏa mãn điều kiện gì?
Sơ đồ hiện và ẩn
Các sơ đồ thiết lập đến giờ đều là sơ đồ hiện (explicit scheme), theo nghĩa trong mỗi phương trình, đại lượng duy nhất ở bước thời gian kế tiếp cần dự tính chỉ là . Với đặc điểm này, sơ đồ hiện có ưu điểm là ta có thể giải ngay mỗi phương trình để tìm ra nghiệm. Ngược lại, trong sơ đồ sai phân ẩn (implicit scheme), cần kết hợp tất cả các phương trình ở nút lưới mới có thể tìm được các giá trị. Điều đó dẫn đến giải hệ PT tuyến tính cho các với ma trận hệ số thường là ma trận thưa với các phần tử khác 0 nằm gần đường chéo chính.
Chẳng hạn với phương trình khuếch tán, một sơ đồ ẩn có dạng: Riêng dạng này còn được gọi là sơ đồ toàn ẩn (fully implicit scheme), với tất cả các đạo hàm theo không gian đều được sai phân tại lớp thời gian kế tiếp (). Sơ đồ này gọi là BTCS, đối lập với sơ đồ FTCS trong sơ đồ hiện.
Dạng tổng quát hơn với sai phân của PT khuếch tán là: Hệ số () thể hiện mức độ “ẩn” của sơ đồ. ứng với sơ đồ hiện, : sơ đồ ẩn, và riêng : toàn ẩn. Đặc biệt, với , trọng số của các giá trị ở lớp thời gian và là như nhau. Sơ đồ như vậy có tên là Crank-Nicolson, còn gọi là CTCS.
Phương pháp tách thời gian MacCormack
Phương pháp đơn giản này cho độ chính xác cao (bậc 2 cả trong không gian lẫn thời gian) [@Lin2008], nhưng cũng như các lược đồ sai phân trung tâm trong không gian (Lax-Wendroff và Crank-Nicolson), một nhược điểm là có thể gây xuất hiện nhiễu động giả (spurious).
Phương pháp được thực hiện qua hai bước (“dự đoán - hiệu chỉnh”). Ở bước “đoán”, một giá trị sơ bộ, , được tính ra. Giá trị sơ bộ này được chữa lại ở bước hiệu chỉnh, khi đó đạo hàm không gian được lấy trung bình cộng của các sai phân tiến ở lớp thời gian và sai phân lùi ở :
Một dạng của phương pháp tách này là ADI, sẽ được trình bày ở mục 3.9.
Sai phân theo không gian 2 chiều
Từ các sơ đồ sai phân đã xây dựng trong các mục trên có thể dễ dàng mở rộng sang không gian 2 chiều.
Dạng đơn giản nhất là phương trình elip:
Đây là phương trình Poisson, nó có thể dùng để mô tả phân bố nhiệt () hoặc cột nước trong tầng nước ngầm có áp (). Trong trường hợp thứ hai, ý nghĩa của và là độ dẫn thuỷ lực (= const, đơn vị m/s) còn (m/s) là nguồn hoặc điểm rút.
- Khi , ta có phương trình Laplace, .
- Khi const, mà biến đổi theo , thì cần viết lại PT:
Một khó khăn khi sai phân trong bài toán 2 chiều là trong trường hợp biên có dạng hình học phức tạp, ví dụ như trường hợp biên dạng Dirichlet (cho số), xem cuốn sách của Chapra và Canale [@Chapra2005], [công thức (29.23-24)]; tuy nhiên các sai phân như vậy cũng chỉ đạt được độ chính xác cấp 1. Trường hợp biên dạng Neumann (cho đạo hàm) thì còn khó hơn nữa.
Một ví dụ khác về PVR hai chiều; xét phương trình sóng dài và biên độ nhỏ,3 ở dạng đơn giản (bỏ qua ma sát và số hạng chuyển tải):
trong đó là mực nước, là độ sâu nước tĩnh, là các thành phần vận tốc dòng chảy theo phương . PT này có thể được đưa về: , với là tốc độ truyền sóng nước sâu. (Bạn hãy tự biến đổi!) Đó là PT dạng gì? elip, hyperbol hay parabol?
Đối với PT Poisson, sau khi sai phân ta sẽ được hệ phương trình, như trường hợp bài toán điều kiện biên (mục 2.4). Tuy nhiên, cái khác ở đây là không gian 2 chiều sẽ khiến cho mỗi phương trình có 5 ẩn (một nút tại chỗ và 4 nút lân cận). Điều đó dẫn đến một hệ PT 5 đường chéo với ẩn. Ngoài ba đường chéo trung tâm thì hai đường chéo ngoài sẽ cách giữa khoảng hoặc phần tử, tuỳ theo cách lưu các biến ma trận theo các hàng ngang những giá trị hay theo các cột dọc những giá trị . Không có thuật toán như Thomas để giải nhanh hệ này, và do vậy để tránh giải theo cách chính xác (nhưng lâu), người ta thường dùng cách xấp xỉ Gauss–Seidel (Liebmann) (mục 29.2, Chapra & Canale (2005) [@Chapra2005]). Để đẩy nhanh quá trình lặp, người ta có thể dùng cách kéo dãn quá SOR (successive over-relaxation). Để minh hoạ cho cách làm này, xét trường hợp đơn giản, và . Khi đó, phương trình Laplace được sai phân thành:
Việc giải lặp được thực hiện từ và . Cuối mỗi vòng lặp, có thể cập nhật giá trị bằng cách dãn quá: trong đó là giá trị cũ từ lần lặp trước còn là một hệ số dãn.
Sơ đồ ẩn luân hướng (ADI) cho bài toán điều kiện đầu
Trong bài toán điều kiện đầu, việc xây dựng sơ đồ sai phân ẩn cũng dẫn đến một ma trận tương tự. Tuy nhiên, trong trường hợp này người ta thường dùng một phương pháp có tên Alternating-Direction Implicit (ADI, ẩn luân hướng). Theo cách này, mỗi bước thời gian sẽ được chia ra thực hiện bằng hai khâu. Ví dụ như với PT khuếch tán 2 chiều, , ở khâu thứ nhất:
Như vậy, số hạng được sai phân hiện còn thì sai phân ẩn. Ta nhận được một hệ PT 3 đường chéo để giải ra các ở “nửa bước thời gian”. Những trị số này được sử dụng trong khâu thứ hai, ở đó số hạng được sai phân ẩn:
và sau khi giải hệ ta sẽ thu được các . Phương pháp ADI thuộc nhóm các phương pháp “tách” (splitting method).
Phân tích ổn định đối với sơ đồ hiện giải PT khuếch tán parabol 2 chiều; so sánh điều kiện ổn định với kết quả phân tích bài toán 1 chiều.
Phương pháp thể tích hữu hạn
Phương pháp thể tích hữu hạn (FVM) có thể áp dụng được cho các PT vi phân biểu diễn các dạng định luật bảo toàn. Ưu điểm của nó là có thể dùng được cho miền có dạng hình học bất kì và hỗ trợ cả lưới tính toán cấu trúc lẫn phi cấu trúc. Trong phương pháp FVM:
- Miền tính toán được chia thành các phần tử riêng biệt gọi là các thể tích kiểm soát (control volume)
- PT vi phân sẽ được tích phân để thành dạng một phương trình cân bằng đối với mỗi thể tích kiểm soát; sau đó các tích phân này được xấp xỉ bằng phương pháp số trị.
Đặc điểm quan trọng của FVM là thông lượng được bảo toàn từ ô tính toán này sang ô liền kề. Nghĩa là có sự bảo toàn tại chỗ đối với thông lượng. Điều đó rất quan trọng vì thông lượng rất cần thiết khi tính toán thuỷ động lực học.[@Popescu2014]
Một sơ đồ thể tích hữu hạn có thể coi là biểu thức tương đương với sai phân hữu hạn nhưng viết dưới dạng tích phân (chứ không phải dạng vi phân) của các phương trình cơ bản.
Hãy ví dụ bằng bài toán điều kiện biên (BVP) 1 chiều gần giống như mục 2.4. Xét PT vi phân:
Bây giờ, ngoài các điểm nút lưới , ta cần hình dung các thể tích kiểm soát bao quanh mỗi điểm nút (Hình trái của [fig:FVM1]{reference-type=“ref” reference=“fig:FVM1”}). Trong không gian 1 chiều thì thể tích này có dạng một đoạn; chẳng hạn thể tích bao quanh điểm sẽ là đoạn . Khi đó ta lấy tích phân của PT trên đoạn này:
Dùng hai giá trị trung gian cho tham biến và sử dụng quy tắc “điểm giữa” để tính hai tích phân ta được:
Từ đó đưa về phương trình:
Có thể thấy rằng đây là hệ 3 đường chéo đối xứng với .
Bài tập. Cho thấy rằng PT sai phân [discr-FVM-BVP] cũng đạt độ chính xác cấp 2.
Mở rộng bài toán cho trường hợp 2 chiều, xét bài toán điều kiện biên (với là biến lượng):

Hình. Phân định thể tích kiểm soát bao quanh mỗi điểm nút [@Popescu2014]. Bên trái: lưới 1 chiều. Bên phải: lưới 2 chiều.
Để thích hợp với bài mới, ta xét trường hợp 2 chiều với lưới điểm nút (Hình phải của [FVM1]). Mỗi điểm sẽ được bao quanh bởi “thể tích kiểm soát” (CV) là hình chữ nhật . Diện tích của hình chữ nhật này bằng (dĩ nhiên bằng trong trường hợp lưới đều). Lấy tích phân trên miền chữ nhật này theo cách tương tự như PT một chiều [BVP-1D-int]. Nhưng lần này tích phân của các biểu thức ngoặc vuông không thể được thay cận một cách dễ dàng nữa. Ta cần dùng một công cụ: định lý Gauss (Ostrogradsky). Với vec-tơ biến lượng:
thì hai số hạng đầu trong PT [eq:BVP-2d] sẽ là4: . Định lý Gauss cho phép chuyển từ tích phân miền sang tích phân biên:
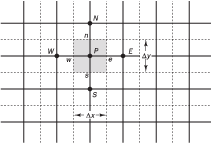
Hình. Vị trí các nút lân cận, các điểm giữa của 4 mặt một thể tích kiểm soát trên lưới
Tích phân vế phải tiện cho tính toán vì biên chỉ gồm 4 đoạn thẳng là 4 cạnh của miền chữ nhật . Chẳng hạn với mặt “bên phải” hay “phía đông (e)” (Hình [grid]), số hạng của tích phân là: = (hình chiếu của vec-tơ trên trục . Như vậy, thừa số thứ nhất đã được tính tại điểm e (điểm ) với sai phân trung tâm có độ chính xác cấp hai.
Tương tự, có thể tính các số hạng còn lại cho các cạnh s, w, n. Hai số hạng còn lại, và .
Ở đây, cần giả thiết rằng phân bố đều trong ô còn mỗi thông lượng phân bố đều trên từng mặt bên.
Ví dụ trên cho thấy FVM hoạt động tốt trên lưới chữ nhật, cũng như phương pháp sai phân hữu hạn. Tuy nhiên lợi thế của FVM thấy rõ khi các ô tính bị biến dạng (đặc biệt là tại biên) hoặc một phần cạnh ô bị chặn thông lượng qua. FVM còn có ưu điểm là cho phép lập các lưới phi cấu trúc, giúp tính toán trên những vùng có dạng đường biên phức tạp và những bài toán yêu cầu làm mịn lưới một cách linh hoạt. Trong mọi trường hợp, định lý Gauss đều cho phép xây dựng công thức mà không cần phải quy về các phương .
Biểu diễn thông lượng. PT cân bằng thông lượng như một tổ hợp tuyến tính các biến lượng. Từ PT khuếch tán, có thể dùng FVM đẻ đưa về phương trình tuyến tính, ví dụ như PT [FVM-1D], và có thể dễ dàng mở rộng sang trường hợp 2 chiều. Trong trường hợp có số hạng nguồn , người ta thường tuyến tính hóa số hạng này dưới dạng . Khi đó phương trình cân bằng cho biến lượng đối với thể tích kiểm soát sẽ được đưa về dạng: , trong đó chỉ số nb là để chỉ các ô lân cận (N, S, E, W).
Hãy viết PT tuyến tính liên hệ biến lượng tại các CV áp dụng cho trường hợp PT [BVP-2d]. Gợi ý: số hạng nguồn là (). Sau đó cho thấy rằng các hệ số chỉ phụ thuộc vào ; còn .
Hệ PT Navier-Stokes cho chất lỏng không nén
Xét hệ PT Navier-Stokes 2D cho chất lỏng không nén được ( const), thường dùng trong thuỷ khí động lực công nghiệp: Hệ PT này có ba ẩn . Việc không xuất hiện trong phương trình đầu gây khó giải. (Thật ra, giá trị cụ thể của không quan trọng, miễn là các gradient của theo đúng là được.) Để giải hệ này, người ta thường tách PT động lượng bằng cách ban đầu là tính trường vận tốc () mà không xét đến áp suất, chẳng hạn với : trong đó các đạo hàm theo không gian được sai phân theo cách phù hợp.
Sau đó, áp suất sẽ được bổ sung vào:
Trị số áp suất được xác định từ phương trình Poisson dưới đây. Bằng cách xây dựng PT này, trị số vận tốc trong lớp thời gian tới thoả mãn được điều kiện .
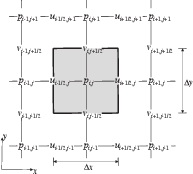
Hình. Lưới tính toán cùng thể tích kiểm soát cho điểm tính áp suất [@Tryggvason2016]
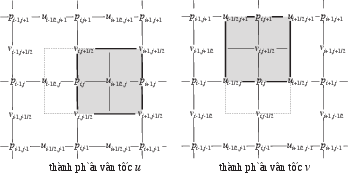
Hình. Thể tích kiểm soát cho các điểm tính vận tốc [@Tryggvason2016]
Trong việc giải hệ PT vi phân [NS-incompr], nhiều nghiên cứu cho thấy rằng nếu ta dùng lưới tính thông thường mà trên mỗi nút lưới có cả ba giá trị () (lưới đồng vị, colocated grid), thì kết quả tính sẽ xuất hiện dao động áp suất xen kẽ kiểu “ô bàn cờ”. Để khắc phục, người ta dùng lưới đan xen (staggered grid), trong đó các điểm nút lưới của , của , của được xếp xen kẽ nhau theo quy tắc bao quanh một điểm nút thì có hai nút ở hướng Đông-Tây còn hai nút ở hướng Nam-Bắc (Hình [staggered-puv]). Thể tích kiểm soát cho nút được thiết lập cắt qua lưới sao cho các điểm nút và nằm đúng tại trung điểm của bốn cạnh khối thể tích kiểm soát này.
Tương tự đã làm ở PT [eq:Gauss], ta lấy tích phân PT liên tục div u = 0 để nhận được: . Sự có mặt của thành phần vận tốc chính giữa các cạnh thể tích kiểm soát (CV) cho đòi hỏi phải có những CV mới cho các nút và này; những CV như vậy () dịch chuyển đi nửa ô lưới so với CV của (Hình [fig:staggered-uv]). Tích phân của động lượng () cho CV của như sau: và tương tự, với CV của : Các trị số vận tốc trên mặt biên CV trong hai xấp xỉ trên thường không được quy định sẵn, bởi vậy cần phải nội suy bằng trung bình cộng các trị số gần kề.
Các thông lượng khuếch tán qua các cạnh bên của CV vận tốc được tính với đạo hàm lấy bằng sai phân trung tâm, tương tự như PT [BVP-1D-int]. Chẳng hạn, với CV của :
Từ đó số hạng khuếch tán sẽ được biểu diễn dưới dạng như sai phân trung tâm bậc 2 quen thuộc. Các PT tính do đó sẽ là:
Tích phân số hạng áp suất trên các CV của :
Từ đó tính được các vận tốc chỉnh sửa:
Thay các PT trên vào bảo toàn khối lượng (div u = 0), ta được:
Hệ PT áp suất có thể được giải theo một số cách, như phép lặp SOR.
Cách sai phân trung tâm ở các số hạng chuyển tải (động lượng) cho sơ đồ với độ chỉnh xác cấp 2; tuy nhiên nhược điểm của nó là với chất lỏng không nhớt, sơ đồ sẽ không ổn định. Hãy viết tích phân các số hạng này theo dạng ngược dòng. Có thể tham khảo http://www.mathematik.uni-dortmund.de/~kuzmin/cfdintro/lecture5.pdf
Xử lý biên
Tại các biên, để tính được các đạo hàm với độ chính xác cần thiết, người ta thường lập nên một vùng đệm với những điểm nút ảo cho (Hình [ghost-cell]). Với việc mở rộng vùng đệm này, miền tính cho các đại lượng sẽ có kích thước: .
Biên của mô hình không cho nước đi qua; ĐK biên đối với vận tốc là: thành phần vận tốc pháp tuyến với mặt biên bằng 0. Với các biên có dạng hình học đơn giản, ĐK này đồng nghĩa với thành phần vận tốc ( hoặc ) phải bằng 0. Thành phần vận tốc tiếp tuyến tại biên bằng trung bình cộng giữa các vận tốc nút ảo và một nút trong miền tính. Chẳng hạn, với biên phía dưới, . Như vậy tại biên này, thành phần vận tốc tại các nút ảo sẽ bằng: ; đây là cách để đưa số liệu ĐK biên vào lưới tính.
Biên không trượt. Với các chất lỏng có độ nhớt, yêu cầu dòng chảy tại biên là “không trượt” (non-slip), giá trị vận tốc tiếp tuyến tại biên = 0. Tuy nhiên, khi biên không nằm dọc đường kẻ lưới thì phải chọn giá trị của nút ảo bằng số đối của giá trị nút trong miền: .
![[[fig:ghost-cell]]{#fig:ghost-cell label="fig:ghost-cell"}](http://coastal-study.uk/bookfig/pps/ghost_cell1-crop.png)
Hình. Các điểm nút ảo để thiết lập điều kiện biên [@Tryggvason2016]
Bài tập. Xét bài toán “khoang có nắp trượt” (lid-driven cavity). Miền tính toán vuông (Hình [cavity]) có kích thước (trong các bài toán CFD, PT phi thứ nguyên thường được dùng với giá trị một số đại lượng được chọn bằng đơn vị); nắp trượt với vận tốc bằng 1. Số ô lưới được chọn là với bước thời gian phù hợp. Sử dụng mã lệnh download về từ đường link notebooks/Navier-Stokes-2D.ipynb [@Tryggvason2016]. Chạy chương trình, sau đó thay đổi các thông số như và độ phân giải. Nhận xét kết quả tính toán. So sánh với kết quả mô phỏng của Ferziger & Perić [@Ferziger2002] trên Hình [cavity].


Hình. Bài toán khoang có nắp trượt. Phía dưới là kết quả tính các profile lưu tốc tại đường thẳng đứng qua giữa khoang với các độ phân giải lưới khác nhau [@Ferziger2002].
Biên hình học phức tạp. Loại biên đơn giản nhất về hình học là các đường biên trùng với cạnh miền chữ nhật. Trong thực tế, điều này thường không được thoả mãn. Tùy tình hình mà ta cần bổ sung các điểm ảo vào trong ma trận để thể hiện biên này.
Bài tập. Trong khoang vuông, người ta lấp đi một góc phần tư phía dưới bên phải. Hãy chỉ định ĐK biên phù hợp.
Mô hình thủy động lực 2D cho vùng biển
Vùng ven bờ biển là vùng có động thái thủy lực phức tạp, có sự tương tác giữa sóng và dòng chảy, là nơi dòng chảy chịu tác động mạnh mẽ bởi ma sát đáy, có rối động và tiêu tán năng lượng mạnh do sóng vỡ. XBeach [@Roelvink2009] là một trong số các mô hình số trị được phát triển nhằm mô phỏng được những quá trình đó. Trong mô hình có hai phần (module) cơ bản là tính sóng và dòng chảy. Để đơn giản, trong mục này ta chỉ xét module dòng chảy, còn ảnh hưởng của sóng được đưa vào thông qua đại lượng ứng suất phát xạ (radiation stress). Các giá trị vận tốc trung bình theo độ sâu () cũng được lấy trung bình theo chu kì sóng.
Hệ phương trình nước nông có dạng:
trong đó là hệ số Coriolis, const với vùng biển nhỏ. Độ nhớt trong các PT biểu diễn độ nhớt xoáy trong PT Navier-Stokes. Độ sâu nước bằng hiệu giữa mực nước và cao trình đáy, .
Bài tập. Xét dạng rút gọn của hệ PT trên khi bỏ qua các số hạng đối lưu, ma sát và độ nhớt rối. Người ta thực hiện sai phân hiện như sau:
Giả thiết rằng độ sâu = const, , hãy dùng cách thay thế để cho thấy rằng sơ đồ trên luôn bất ổn định [@Dyke2007].
Để đảm bảo cho mô hình được ổn định, lưới đan xen đã được sử dụng trong XBeach (tương tự như Hình [staggered-puv]), nhưng ở tâm của ô bây giờ là mực nước và độ sâu .
PT liên tục được viết dạng tích phân cho CV của là:
Phương pháp ngược dòng được sử dụng với các số hạng chuyển tải. Giá trị các thành phần vận tốc tiếp tuyến tại trung điểm các cạnh được tính bằng trung bình cộng các thành phần vận tốc tương ứng ở lân cận: và .
Các độ sâu tại trung điểm cạnh này phức tạp hơn một chút. Độ sâu phục vụ cân bằng động lượng () thì đơn giản bằng trung bình cộng độ sâu tâm 2 CV kề bên: và . Trong khi đó độ sâu cho cân bằng khối lượng thì lại lấy bằng độ sâu của ô “thượng nguồn” nếu như vận tốc dòng chảy vượt ngưỡng hoặc ; còn không thì bằng hiệu giữa mực nước cao hơn trừ cao trình đáy cao hơn trong số 2 ô kề bên.
Bài tập. Hãy viết biểu thức xấp xỉ số hạng độ dốc mặt nước trong phương trình.
Có hai số hạng nguồn. Số hạng lực Coriolis có dạng tuyến tính đơn giản, và ma sát đáy là số hạng phi tuyến bậc hai. Để cho đơn giản, sai phân tiến (Euler) được sử dụng cho số hạng này.
Trong thực tế, khai triển biểu thức ứng suất tiếp tại đáy, ta nhận được số hạng ma sát theo hai phương là ; trong đó là một hệ số ma sát.
Điều kiện biên hở
Tốt nhất là nên bố trí biên của mô hình trùng với biên vật lý, nhưng nhiều khi ta không tránh khỏi việc phải đặt biên “mở” ở một tuyến bất kì trong thủy vực. Khi đó, cần quy định những ĐK tại biên của miền để phỏng theo sự tồn tại của khối nước xung quanh. Những ĐK biên này cần cho phép các nhiễu động hướng ra ngoài đi xuyên qua biên mà không tạo những phản xạ sai truyền ngược vào trong miền [@Durran2010].
Đối với XBeach, chế độ mặc định của điều kiện biên được dựa trên phương pháp đường đặc tính, cho phép các sóng dài đến theo phương chéo biên, do đó thích hợp với các bài toán 2D [@Roelvink2008].
Sử dụng bản mầu mã lệnh (đơn giản) của XBeach và bổ sung các thành phần khuếch tán rối, độ dốc mặt nước, lực Coriolis và lực ma sát đáy. Thiết lập kịch bản với đáy địa hình đơn giản, một biên (hở) có mực nước dao động, chạy chương trình và quan sát kết quả.
Vấn đề nhiễu
Khó khăn với người mới bắt đầu lập chương trình dựa trên phương pháp số là khi gặp phải nhiễu, mà nghiệm số dao động không như mong muốn. Những thứ quan trọng nhất cần kiểm tra khi đó bao gồm: bước thời gian, độ dài ô lưới, các điều kiện biên và quá trình lặp.[@Wood1993]
-
Bước thời gian. Việc dùng các phương pháp nhiều bước có thể gây nên nghiệm giả (spurious); cố gắng sử dụng sơ đồ loại một bước. Trong các sơ đồ ẩn, loại chính xác nhất là Crank-Nicolson (). Nhưng loại này có nhược điểm là tạo nên dao động với các lớn (gọi là hiệu ứng răng cưa Crank-Nicolson). Có thể kiểm soát điều này qua việc giảm . Lấy sẽ làm giảm dao động và làm mất dao động song kết quả sẽ kém chính xác.
-
Chiều dài cạnh ô lưới. Khi khoảng cách nút lưới hoặc cạnh phân tử quá lớn đều có thể gây nên sự dao động của nghiệm số trong không gian mà lẽ ra tại đó nghiệm chỉ đơn điệu tăng hoặc giảm. Hiện tượng này có thể gắn với số Péclet ô lưới. Với các bài toán phụ thuộc thời gian thì kết quả tính với lưới thô sẽ không cải thiện kể cả khi chừa thời gian cho giai đoạn khởi động mô hình.
-
Điều kiện biên. Vấn đề có thể xảy ra khi có bước thay đổi đột ngột trong điều kiện biên. Đôi khi điều kiện biên Dirichlet bị đưa nhầm dấu; nước dồn lên hoặc biến mất một cách phi lý chính là một biểu hiện. Các biểu hiện kì lạ khác của một mô hình bần sát biên có thể cho thấy rằng biên phải được đặt xa hơn, hoặc điều kiện biên không phù hợp. Các sơ đồ ẩn luân hướng (ADI) với biên dị thường có thể gây vấn đề khó khắc phục.
-
Điều kiện đầu. Mô hình có thể phải chạy khởi động một thời gian để nhiễu động biến mất, khi đó hệ thống đạt đến trạng thái ổn định động lực thì kết quả số trị mới có ý nghĩa.
-
Quá trình lặp. Các nhiễu động xảy ra theo lần lặp cho thấy cần phải thực hiện giãn dưới (under-relaxation).
Phụ lục: Cài đặt và lập trình Julia
Bạn cần một máy tính PC với đường truyền Internet thật tốt. Tải về bộ cài Julia (tuỳ theo hệ điều hành và loại hệ 32/64-bit) từ trang web http://julialang.org. Sau đó chạy chương trình cài đặt và gõ lệnh julia (trong Linux) hoặc kích vào biểu tượng Julia (Windows). Một cửa sổ câu lệnh hiện ra. Gõ vào lệnh sau: using Pkg; Pkg.add("IJulia")
rồi gõ Enter (để thực hiện lệnh). chờ một lúc cho máy thực hiện cài đặt…
Ngoài ra, để vẽ được đồ thị, cần cài đặt thư viện PyPlot theo cách tương tự với câu lệnh Pkg.add("PyPlot")
Sau khi việc cài đặt hoàn tất, máy sẽ chờ gõ lệnh tiếp. Lần lượt gõ vào hai lệnh:
using IJulia
notebook()
Trình duyệt web sẽ hiện ra và có thể thấy danh sách các file và thư mục. Mã lệnh Julia có thể được tạo mới bằng cách chọn nút [New - Julia]. Một cửa số mới được mở ra và bạn có thể nhập vào mã lệnh Julia, thực hiện và tính toán kết quả. Trong giao diện này (notebook), mã lệnh được nhập vào các ngăn (cell) và từng ngăn có thể được thực hiện (bằng cách ấn Ctrl+Enter hoặc Shift+Enter). Một ngăn cũng có thể được dùng để ghi văn bản (bằng cách chọn [Markdown] thay cho [Code]).5
Nội dung của quyển tập lệnh (notebook) có thể được lưu vào một file *.ipynb, với định dạng cấu trúc theo kiểu JSON, trong đó có đầy đủ các đoạn mã lệnh, các thuyết minh bằng Markdown. Các hình vẽ từ biểu đồ được mã hoá thành các kí tự dưới dạng PNG.
Julia hỗ trợ đầy đủ phép toán (+ - * / \^), cả với số phức, ví dụ (5 - 3im)*4im. Nhiều hàm toán học tương tự như ở Matlab, đặc biệt với các hàm ma trận. Song khác với Matlab, kí hiệu phần tử của ma trận là ngoặc vuông chứ không phải ngoặc tròn, chẳng hạn A[5:end,3].
Trong kí hiệu trên, dấu hai chấm thể hiện dãy số, từ 5, 6, đến thứ tự dòng cuối của ma trận. Dãy cũng có thể chạy ngược ví dụ end:-1:5. Dãy có thể được dùng trong vòng lặp for, như ở bài tập PP Thomas.
Sử dụng cách kí hiệu phần tử, ta có thể dễ dàng triển khai những sơ đồ sai phân bằng câu lệnh Julia. Thật vậy, với sơ đồ FTCS cho bài toán khuếch tán, , có thể dễ dàng viết lệnh:
F[j] += D*DT/(2DX^2) * (F[j-1] - 2*F[j] + F[j+1])
trong đó kí hiệu += có tác dụng “cập nhật” biến số bên trái bằng cách cộng vào thêm giá trị tính được từ vế phải.
Vec tơ và ma trận có thể khởi tạo bằng lệnh gán với các phần tử ghi trong cặp ngoặc vuông, ví dụ [1 3; 5 6] là ma trận . Tuy nhiên với ma trận lớn, cần khởi tạo bằng lệnh kiểu như zeros:
V = zeros(N, 1)
M = zeros(N, NT)
Để vẽ các đường thể hiện sự thay đổi của biến lượng theo không gian và thời gian, có thể dùng PyPlot:
using PyPlot
plot(V)
plot(M[:,1])
Ở đây đã vẽ biểu đồ thể hiện sự thay đổi của vec-tơ V theo thứ tự phần tử (1:N), và vẽ giá trị của cột thứ nhất thuộc ma trận M.
Trong các bài toán 2 chiều, để lưu kết quả trường dòng chảy (dù phải tốn bộ nhớ máy), ta cần lập mảng 3 chiều, chẳng hạn:
A = zeros(NX, NY, NT)
Để biểu thị kết quả, ta nên lập các ma trận toạ độ X và Y. Kết quả tính toán thường được thể hiện dưới dạng biểu đồ màu với đại lượng vô hướng như mực nước (Z) và biểu đồ mũi tên với đại lượng vec tơ như vận tốc (U, V), chẳng hạn:
for i = 1:NX
for j = 1:NY
X[i,j] = (i-1)*DX; Y[i,j] = (j-1)*DY
end
end
# ... thực hiện tính toán ...
using PyPlot
pcolor(X, Y, Z)
quiver(X, Y, U, V)
Sau cùng, quyển tập lệnh có thể được upload lên máy chủ web của bạn và dùng đường link đó để xem trực tuyến bằng dịch vụ Jupyter Notebook Viewer (nbviewer.jupyter.org). Nếu không có máy chủ web, bạn có thể gửi lên Dropbox và lấy link.
Tài liệu tham khảo
Anderson, J.D. (1995) Computational Fluid Dynamics: the Basics with Applications, McGraw-Hill.
Chapra, S.C. (1997) Surface Water-Quality Modeling, McGraw-Hill. Có bản dịch tại trường ĐH Thuỷ lợi.
Chapra, S.C., Canale, R.C. (2005) Numerical Methods for Engineers, McGraw-Hill. Có bản dịch “Phương pháp số cho kĩ sư” tại trường ĐH Thuỷ lợi.
Dalhquist, G., Björck, A. (1974) Numerical Methods, Prentice Hall.
Durran, D.R. (2010) Numerical Methods for Fluid Dynamics: with Applications to Geophysics, 2nd Edition, Springer.
Dyke, P. (2007) Modelling Coastal and Offshore Processes, Imperical College Press.
Ferziger, J.H. (1981) Numerical Methods for Engineering Applications, Wiley.
Ferziger, J.H., Perić, M. (2002) Computational Methods for Fluid Dynamics, 3rd edition, Springer.
Hearn, C.J. (2008) The Dynamics of Coastal Models, Cambridge Univ. Press.
Lin, P. (2008) Numerical Modeling of Water Waves, Taylor Francis.
Popescu, I. (2014) Computational Hydraulics: Numerical Method and Modelling, IWA Publishing.
Ramshaw, J.D. (2011) Elements of Computational Fluid Dynamics, Imperial College Press.
Roelvink, D., Reniers, A., van Dongeren, A., van Thiel de Vries, J., Lescinski, J., McCall, R. (2008) “XBeach model description and manual 2.0”, Technical Report, UNESCO-IHE, Deltares, TU Delft, Univ. Miami.
Roelvink, D., Reniers, A., van Dongeren, A., van Thiel de Vries, J., McCall, R., Lescinski, J. (2009) “Modelling storm impacts on beaches, dunes and barrier islands”, Coastal Engineering 56, 1133–1152.
Tryggvason, G. (2016) Computational Fluid Dynamics, trong cuốn sách Fluid Mechanics (Kundu, P., Cohen, I.M., Dowling, D.R.), Academic Press.
Versteeg, H., Malalasekra, W. (2007) An Introduction to Computational Fluid Dynamics, Pearson.
Vreugdenhil, C.B. (1989) Computational Hydraulics: an Introduction, Springer.
Wood, W.L. (1993) Introduction to Numerical Methods for Water Resources, Oxford.
PT vi phân này có dạng hyperbol, (hãy tự biến đổi toán học), và do đó theo các phân loại ở PVR tổng quát. ↩︎
Một số tương tự là Reynolds, chỉ khác đại lượng thay cho ; cần nhớ rằng độ nhớt chính là thể hiện cho sự khuếch tán động lượng chất lỏng. ↩︎
Giả thiết rằng biên độ dao động mặt nước nhỏ hơn hẳn so với độ sâu rất quan trọng để tuyến tính hoá PT liên tục. Thật vậy, dạng đúng của PT liên tục là , trong đó độ sâu tổng . Tuy nhiên, ta luôn có thể chọn mặt chuẩn trùng với mực nước trung bình [@Hearn2008] để trong những điều kiện cụ thể có được . Do không phụ thuộc vào nên có thể được đưa ra ngoài đạo hàm, và ta nhận được PT đã tuyến tính hoá. ↩︎
Với trường vec tơ u = () thì divu được định nghĩa là . Còn có thể viết thay cho divu, trong đó toán tử nabla ↩︎
Cú pháp của ký pháp Markdown có thể xem từ các trang web hướng dẫn, chẳng hạn http://eherrera.net/markdowntutorial/ ↩︎