Dùng cho Khóa 54B [PONA 417] năm học 2015-2016.
Bản chỉnh sửa 1/2017
Chuyển online 3/2020

Biên soạn: GV Nguyễn Quang Chiến

Bộ môn Quản lý tổng hợp vùng ven biển: Tầng 3 nhà C1
Trường Đại học Thủy lợi
Số 175 Tây Sơn, Đống Đa, Hà Nội

Khái quát chung

Vận tải đường biển là hình thức chuyên chở có từ thời xưa và đến nay vẫn được coi là hình thức vận chuyển hàng hoá có chi phí rẻ nhất. Những quốc gia nằm giáp biển, có những hải cảng lớn thường đồng thời có nền kinh tế phát triển mạnh. Dễ thấy “Cảng và vận tải biển” là một môn học quan trọng đối với sinh viên chuyên ngành kĩ thuật biển.

Vậy các bạn sinh viên cần tìm hiểu những gì trong khoá học 30 tiết này? Cảng và vận tải biển nói chung là một vấn đề quá rộng; không chỉ có vấn đề thiết kế công trình, phân tích ảnh hưởng đến môi trường, mà còn là điều hành hoạt động của tàu ra vào cảng, tối ưu hoá việc xếp dỡ hàng hoá, đảm bảo an ninh về cảng, và nhiều khía cạnh khác nữa. Vì vậy mục đích của ta là cố gắng lựa chọn để tìm hiểu một số khía cạnh điển hình, có liên quan đến những môn học khác trong chương trình đào tạo kĩ sư chuyên ngành. Cụ thể, ta sẽ tập trung vào ba nhóm chủ đề sau:

• Cấu trúc cơ bản của cảng biển. (Ta không đề cập đến cơ sở hạ tầng bốc xếp vận chuyển trong phạm vi khoá học này.)

• Chế độ thuỷ động lực: sóng và dòng chảy ở khu vực bể cảng và vùng nước lân cận phía ngoài,

• Chuyển động của tàu thuyền tham gia giao thông trong vùng cảng (khó)

Mặc dù các khoá học ít nhiều đều mang lại kiến thức cho sinh viên, tác giả thấy rằng trong hiện nay những kĩ năng và phương pháp mới là thứ đáng học hỏi, rèn luyện trong trường đại học. Bởi vậy, sinh viên cần lưu ý rằng khoá học này có một số đặc điểm sau:

• Rèn luyện kĩ năng là chính; kiến thức có thể tự học được qua việc tham khảo tài liệu. Chính vì vậy, phạm vi môn học đã được rút gọn tối đa.

• Có liên hệ chặt chẽ với những môn học trước, sinh viên có thể áp dụng kiến thức kĩ thuật bờ biển nói chung để giải quyết một những vấn đề cụ thể về cảng biển.

• Phát huy khả năng lập luận, phân tích hệ thống, diễn giải cơ chế và vận hành của tổ hợp công trình (ở đây là cảng biển). Sinh viên cần nhớ thuộc lòng một số ít những công thức cơ bản, có ý nghĩa về mặt vật lý. Những công thức này thường có dạng toán học đơn giản và dễ áp dụng. Bên cạnh đó, khả năng giải thích và diễn đạt bằng hình ảnh sẽ được phát huy để đáp ứng yêu cầu về nghiệp vụ.

• Để đạt hiệu quả trong học tập, sinh viên cần phải mang theo máy tính tay trong mọi tiết học. Việc rèn luyện tính toán kĩ năng tính toán là thiết yếu. Ngoài ra, năng lực của người kĩ sư là phải biểu diễn được điều kiện tự nhiên và công trình, tìm được những nhân tố chi phối, so sánh được các hệ thống với nhau; từ đó đưa ra những nhận xét ngắn gọn nhưng chuyên sâu về kĩ thuật một cách độc lập. Đây chính là yêu cầu trong cách đánh giá chất lượng đào tạo hiện đại: trong quá trình thi cử, thí sinh tuyệt đối không được trao đổi và phải giải quyết các vấn đề một cách sáng tạo dựa trên kiến thức đã học.

• Môn học này kết hợp nhiều phương diện của ngành kĩ thuật bờ biển. Sinh viên có thể gặp một số kiến thức mang dáng dấp của các môn học như: cơ sở kĩ thuật bờ biển, sóng gió, công trình bảo vệ bờ, hình thái bờ biển … song cần hiểu được rằng môn học này không lặp lại những kiến thức đó mà vận dụng chúng để giải quyết vấn đề liên quan đến cảng biển.

• Giáo trình dành cho sinh viên khoa Kỹ thuật biển, theo quy định, là cuốn Vận tải thủy do GV Nguyễn Thị Phương Thảo viết; trong đó chứa nhiều kiến thức tổng hợp về chủ đề. Còn tập bài giảng này chú trọng về khái niệm và thiết kế cảng biển (sẽ được nói rõ ngay sau đây). Cũng cần lưu ý rằng bài giảng không hướng dẫn từng bước thiết kế mà chỉ phân tích rõ những đặc điểm của từng yếu tố thiết kế.

• Bài giảng rất ngắn và không thể chứa đựng hết kiến thức của môn học. Sinh viên cần theo dõi và ghi chép trên lớp để bổ sung những ví dụ hoặc giải thích luận điểm trong cuốn này.

Trong việc xây dựng mỗi công trình, cần tiến hành nhiều khâu: từ xác định khái niệm công trình, đến thiết kế, thi công, vận hành, và cuối cùng là phá dỡ (Hình 1). Có thể thấy rằng khâu nào tiến hành càng sớm thì càng có ảnh hưởng lớn đến chi phí của công trình. Bởi vậy xác định đúng các khái niệm từ đầu và thực hiện thiết kế đúng chuẩn mực là cách hiệu quả để giảm thiểu được chi phí công trình.

Hình 1: Mỗi khâu thực hiện có một mức độ ảnh hưởng đến chi phí công trình.

§1. Tuổi thọ công trình

Một khâu quan trọng trong thiết kế công trình cảng là xác định sóng (Hs_tk) và mực nước thiết kế (Z_tk); công việc này có thể xem giáo trình Công trình bảo vệ bờ hay Thiết kế ngẫu nhiên/Lý thuyết độ tin cậy. Với hải cảng, người ta thường quy định chu kì lặp lại và tuổi thọ công trình, nên ta sẽ tìm hiểu những khái niệm này.

Định nghĩa. Chu kì lặp lại là khoảng thời gian trung bình giữa hai sự kiện kế tiếp mà chiều cao sóng lớn hơn hoặc bằng một giá trị chiều cao sóng ý nghĩa cho trước (gọi là chiều cao sóng thiết kế).

Ưu điểm: Đây là cách định nghĩa đơn giản, áp dụng được với đập phá sóng, bến tàu, cảng nhỏ. Chu kì lặp, T_lặp, thường lấy bằng từ 50 đến 100 năm.

Tuổi thọ công trình theo thiết kế, N, không nhất thiết phải bằng T_lặp. N là số năm cần phải trải qua từ khi dự án bắt đầu mà công trình không chịu tác động nào vượt quá tải trọng thết kế của nó (tức là không có H > Hs_tk).

$T_{lặp} = \frac{1}{1 - \left( 1 - P \right)^{\frac{1}{N}}}$ với P là xác suất xuất hiện, 0 < P ≤ 1.

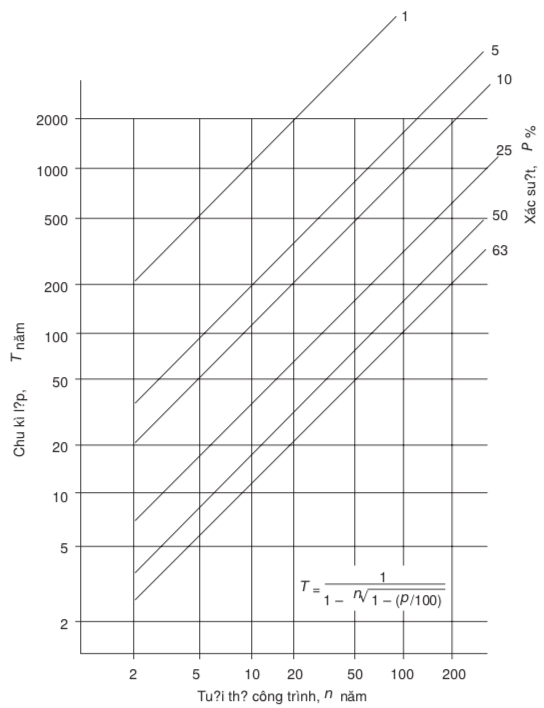
Hình 2. Biểu đồ liên hệ T_lặp, N và P (theo British Standards)

Ví dụ. Bến cảng có tuổi thọ thiết kế 50 năm. Nếu xác suất có sóng cao vượt là P = 10% thì T_lặp cần phải bằng khoảng 500 năm. Nếu chọn T_lặp = N = 50 năm thì biểu đồ Hình 2 cho thấy, trong 50 năm tới, có một xác suất lên đến 63% là sóng sẽ có chiều cao vượt thiết kế.

§2. Đập chắn sóng: chọn tuyến sơ bộ

Tuyến đập chắn sóng phụ thuộc nhiều vào hướng sóng. (Hình 3 cho thấy trường hợp hướng sóng tới dao động trong một hình quạt 180° – 40° = 140°.) Ngoài ra cần xét thêm các yếu tố khác:

• Chiều dài đập càng nhỏ càng tốt. Cũng trên Hình 3, hai đầu đặp được đặt ở mũi đá để giảm bớt một phần độ dài.
• Độ sâu dọc theo trục đập (càng ít biến đổi đột ngột thì càng tốt)
• Nguồn khai thác đá ở gần
• Có thể khai thác được những khối đá cỡ lớn
• Nền địa chất ổn định

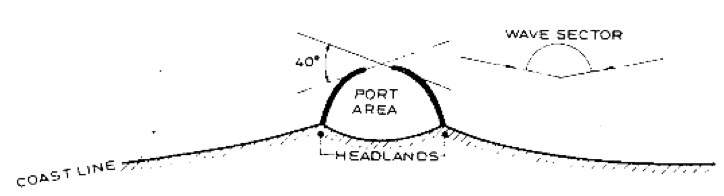
Hình 3. Đập phá sóng và khu cảng trên bờ biển mở (Zhou & Burcharth 2001)

Kích thước của khu cảng phụ thuộc cả vào cách sắp đặt các bến trong cảng; nhưng kích thước tối thiểu nên là: kích thước dọc bờ biển ≥ 6LOA và kích thước vươn xa bờ ≥ 3LOA, với LOA là chiều dài của con tàu chọn để thiết kế. (Kích thước cụ thể của tàu sẽ được trình bày trong §11.)

§3. Một số ảnh hưởng về mặt hình thái bờ biển

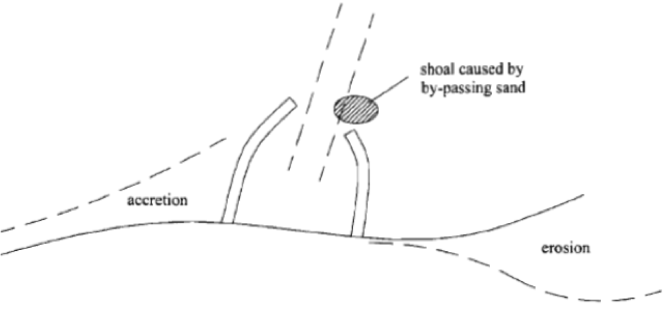
Hình 4. Xói và bồi dọc theo bờ biển sau khi xây đập chắn sóng (Zhou & Burcharth 2001)

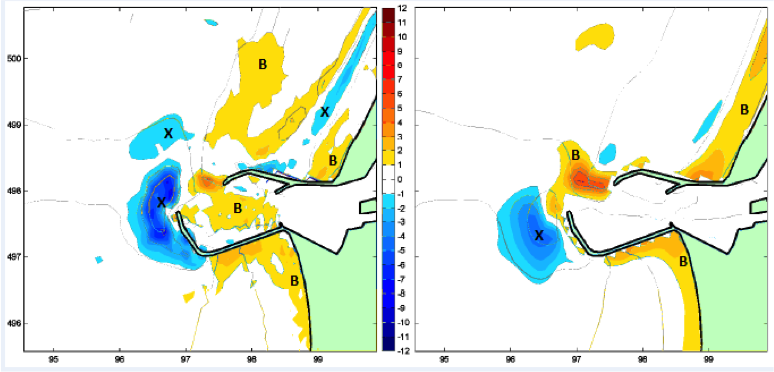
Hình 5. Diễn biến xói-bồi của vùng cảng IJmuiden, Hà Lan (Luijendijk & Walstra 2010)

Khi xây dựng bến cảng, dòng chảy dọc bờ bị chặn lại và nhiều khả năng sẽ hình thành nên hiện tượng bồi lắng và xói lở ở hai phía cảng biển, dẫn tới dạng đường bờ có thể như ở Hình 4.

Hình 5 thể hiện diễn biến bồi lắng / xói lở đáy biển ở vùng lân cận cảng biển IJmuiden. Hình bên trái là tổng hợp từ số liệu thực đo. Hình bên phải là kết quả chạy mô hình thủy động lực hai chiều, Delft3D với thời đoạn mô phỏng dài 8 năm (từ 1968 đến 1976). Có thể thấy rằng mô hình đã dự đoán định tính được xu thế bồi lắng ở đoạn bờ biển sát gốc hai đập và hố xói ngay ngoài đoạn gấp khúc của đập phá sóng dài hơn.

Việc tính toán của mô hình thủy động lực và diễn biến hình thái hai chiều cho kết quả chi tiết trên toàn bộ mặt đáy biển trong khu vực lân cận cảng. Tuy nhiên, kết quả này cũng có thể dùng để suy ra diễn biến vị trí của đường bờ khi coi, chẳng hạn, đường bờ là đường đồng mức có độ cao bằng 0.

§4. Một số ảnh hưởng về chất lượng nước

Cùng với diễn biến hình thái, chất lượng nước là yếu tố cấu thành môi trường quanh vùng cảng. Trước hết, sự tồn tại của những công trình lớn như đập phá sóng gây ảnh hưởng đáng kể tới chế độ mực nước và dòng chảy và sóng trong khu vực. Ngoài ra, sự di chuyển của những con tàu với động cơ lớn gây khuấy động nước và ảnh hưởng nhất định đến lượng bùn cát lơ lửng (và do đó, đến độ sáng và đời sống của hệ thủy sinh). Cuối cùng, một phần ô nhiễm là do rác và nước thải từ tàu xả ra trong quá trình vào cảng.

Việc đánh giá tác động đến chất lượng nước không đơn giản và thường phải dùng công cụ mô hình toán hiện đại dựa trên số liệu đo đạc chi tiết những yếu tố môi trường thuộc vùng dự án.

§5. Tính toán truyền sóng đến vùng cảng

Do tính chất phức tạp của địa hình đáy biển ven bờ và tính ngẫu nhiên của sóng ngoài khơi, cách tốt nhất có lẽ là sử dụng mô hình toán tính sóng dựa theo phổ trên diện rộng. SWAN là một mô hình tiêu biểu. Mô hình này có thể được tích hợp trong bộ phần mềm thủy động lực hai chiều như Delft3D-Flow hay ADCIRC. Những bộ phần mềm khác như MIKE21 có mô hình tính sóng riêng, nhưng về nguyên lý thì gần giống như SWAN.

Phổ sóng là khái niệm quan trọng, do đó cần phải ôn lại tài liệu môn học Sóng gió. Phổ sóng là biểu đồ thể hiện phân bố mật độ năng lượng sóng theo tần số sóng. Nó có vai trò trong quan trắc và tính toán sóng. Nhiều thiết bị đo sóng hiện đại ngày nay cho kết quả đo đạc dưới dạng phổ sóng chứ không phải dưới dạng đường quá trình mực nước theo thời gian, nhờ vậy mà tiết kiệm dung lượng bộ nhớ lưu trữ trong thiết bị và kéo dài thời gian quan trắc. Từ hình dạng phổ sóng có thể suy ra ngay chiều cao sóng ý nghĩa theo công thức H_m0 = 4√m₀ và chu kì sóng đỉnh phổ T_p (thông qua tần số đỉnh, f_p). Trong tính toán sóng thì khi nhập các giá trị H_s và T_p vào biên mô hình (với giả thiết một dạng phổ nhất định), chương trình sẽ thực hiện tính lặp giải hệ phương trình sai phân đối với năng lượng sóng trên toàn miền, từ đó ở các vị trí quan tâm có thể xác định ra H_s và T_p.

Kĩ năng tính toán sóng theo cách thủ công (ví dụ như đã học ở môn Cơ sở kĩ thuật bờ biển) cho phép ta tính truyền sóng đối với sóng đơn có chiều cao và chu kì không đổi, phù hợp với loại sóng lừng. Tuy nhiên, trên biển thường không chỉ có sóng lừng mà (phần quan trọng) còn có sóng do gió. Điều này thể hiện trên phổ sóng (Hình 6).

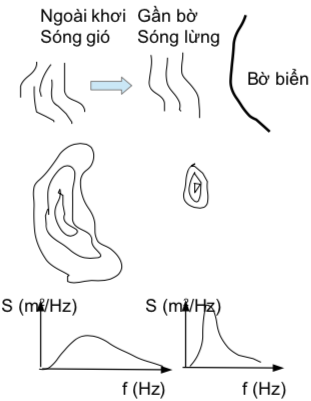
Hình 6. Phổ sóng tại hai điểm đo: xa bờ và gần bờ

Khi tính truyền sóng, cần lưu ý phát hiện và tách riêng thành sóng gió và sóng lừng từ một phổ sóng phức hợp. Việc nhận biết này dễ dàng vì sóng lừng ứng với phần phổ hẹp, nhọn, ứng với f nhỏ hơn và có đỉnh cao hơn. Để tính được chiều cao sóng tổng hợp, các nhà tư vấn ở công ty Norconsult (Na Uy) đề nghị phải tính riêng truyền sóng cho từng phần sóng lừng và sóng gió, rồi xác định chiều cao sóng thiết kế cho công trình: $H_{tổng} = \sqrt{H_{lừng}^{2} + H_{gió}^{2}}$. Công thức này dựa trên cơ sở tổng năng lượng.

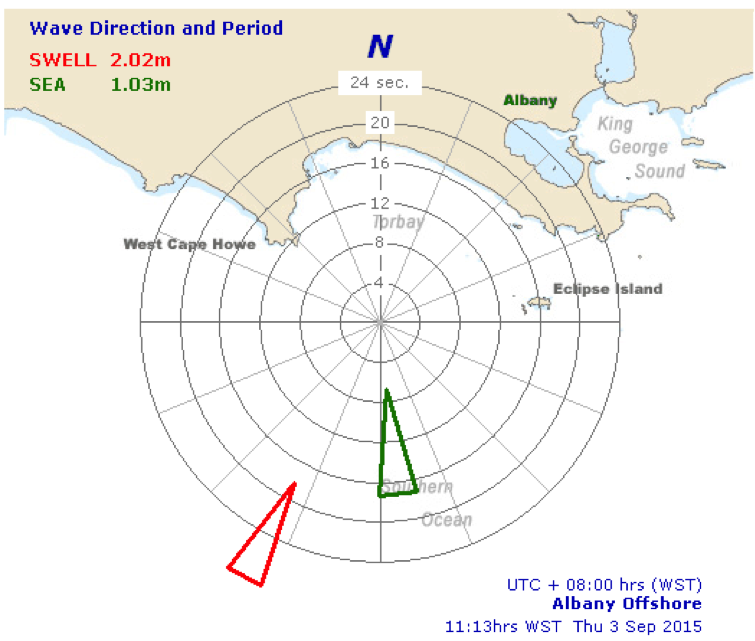
Hình 7: Phân biệt sóng gió và sóng lừng.
Nguồn [http://www.transport.wa.gov.au/imarine/albany-tide-and-wave.asp]

Các đặc trưng sóng nước sâu (H, T) phục vụ tính truyền sóng thì có thể xác định bằng các công thức kinh nghiệm hoặc bằng cách tra biểu đồ, ví dụ Hình 6. Ngoài ra, còn có thể xác định qua việc áp dụng kết quả của các mô hình sóng trên diện rộng như WAVEWATCH-III.¹ Một số dịch vụ web khác như FUGRO ([http://www.oceanor.no/]) cho phép mua số liệu sóng trực tuyến.

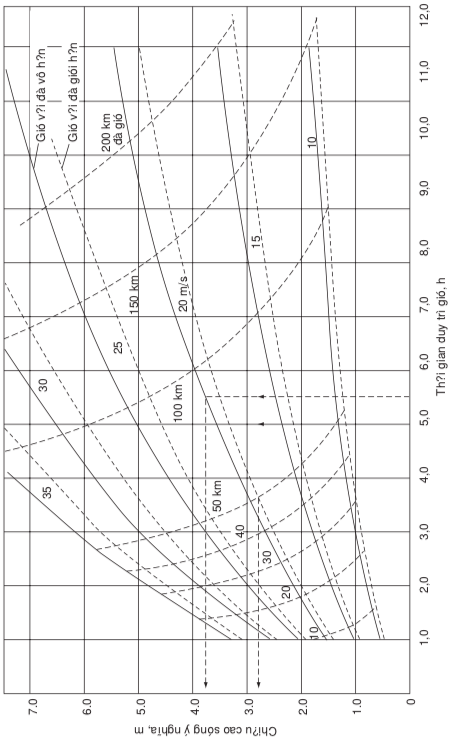
Hình 8: Chiều cao sóng tính từ gió thổi với vận tốc không đổi (Thoresen 2014)

Trong khuôn khổ bài giảng này ta xét phương pháp đồ giải như Hình 8. Cho trước vận tốc gió U, đà gió F, và thời gian duy trì t, tra trên biểu đồ với cùng giá trị tung độ của U ta tìm hai giao điểm với các giá trị tương ứng của F và t. Trong số hai giao điểm này, chọn giao điểm nằm bên trái vì nó có H nhỏ hơn. Nếu giao điểm được chọn này hình thành từ đường dóng của U và F thì ta nói rằng đà gió đã giới hạn sự phát triển của sóng (nên dù gió có thổi lâu đi mấy chăng nữa thì sóng cũng không cao thêm). Ngược lại, nếu giao điểm được chọn hình thành từ các đường gióng của U và t thì thời gian duy trì gió thổi đã giới hạn sự phát triển của sóng.

Bài tập. Bến cảng nằm trong vùng vịnh có đà gió 20 km, tốc độ gió mạnh (20 m/s) duy trì trong 3 giờ. Tra đồ thị để tìm ra chiều cao sóng ý nghĩa và chu kì đỉnh phổ. Kết quả sẽ thay đổi thế nào nếu thời gian duy trì gió chỉ là 1 giờ, hay kéo dài 6 giờ?

§6. Nhiễu xạ sóng

Các tia sóng truyền qua đoạn cửa vào cảng thì bị uốn cong sang hai bên, hướng về phần khuất (phần bị che bởi đập phá sóng). Một phương pháp để xác định chiều cao sóng nhiễu xạ là dùng biểu đồ cornu (xem giáo trình Sóng gió) hoặc thông qua nghiệm giải tích dạng hàm sin/cos Fresnel.² Tuy phương pháp này có cơ sở lý thuyết rõ ràng nhưng cần phải tính toán và không thật tiện và trực quan đối với người kĩ sư.

Do vậy, người ta đã xây dựng các biểu đồ nhằm xác định hệ số nhiễu xạ K_d, hay tỉ lệ chiều cao sóng nhiễu xạ so với sóng tới. Chẳng hạn, các biểu đồ sau đây do HR Wallingford lập cho trường hợp chiều dài sóng tới, L, bằng bề rộng B của đoạn cửa, và xét đến các góc sóng tới bằng 0° (truyền thẳng vuông góc với đoạn cửa), và xiên góc 30°, 45°, 60°.

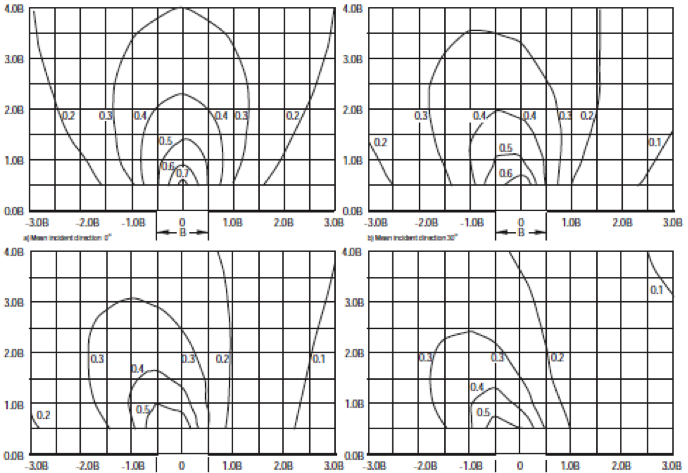
Hình 9. Nhiễu xạ qua đoạn cửa vào cảng với các góc sóng tới khác nhau.

Hình 10. Nhiễu xạ qua đầu đập chắn dài bán vô hạn với sóng tới vuông góc. Trường hợp sóng gió và sóng lừng.

Ngoài ra, còn có biểu đồ sóng nhiễu xạ qua đầu đập chắn sóng dài bán vô hạn (Hình 10). Trong trường hợp này, chỉ phân biệt hai hình thức: sóng gió (biểu đồ trái) và sóng lừng (biểu đồ phải). Lưu ý rằng ở biểu đồ loại này khác biểu đồ loại trước: các tọa độ được tra dưới dạng x/L và y/L thay vì x/B và y/B; ngoài ra, gốc tọa độ ở điểm đầu đập thay vì ở trung điểm của đoạn cửa vào.

Riêng với đập chắn dài bán vô hạn, còn có thể xét trường hợp sóng đến xiên góc một chút; khi đó cần lưu ý xoay trục tọa độ để “đập chắn ảo” vuông góc với hướng sóng tới (Hình 11).

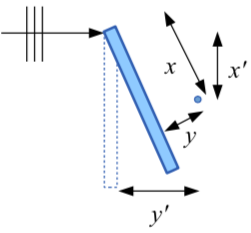
Hình 11. Xoay trục tọa độ trong trường hợp hướng sóng đến không vuông góc với đập. Tọa độ (x, y) → (x′, y′).

§7. Độ lặng sóng trong bến cảng

Sau đây ta xét một ví dụ tính độ lặng sóng cho cảng Akita, Nhật Bản (1974). Số liệu sóng khí hậu được tổng hợp ở Bảng 1, với tần suất tích lũy các cấp sóng theo các hướng khác nhau. Các chu kì sóng cũng được cho tương ứng, chu kì này tăng dần theo cấp sóng.

Bảng 1. Số liệu sóng khí hậu, cảng Akita

Hướng sóng	Tần suất (%)	Chiều	cao	sóng	ý	nghĩa	,	H1/3
		> 0 m	> 1 m	> 2 m	> 3 m	> 4 m	> 5 m	> 6 m
SW	1,4	1,4	0,4	0,1	0	0	0	0
WSW	29,0	29,0	9,2	2,5	1,2	0,5	0,3	0,1
W	68,2	68,2	21,6	6,2	2,8	1,2	0,7	0,2
WNW	1,4	1,4	0,4	0,1	0	0	0	0
Tổng	100,0	100,0	31,6	8,9	4,0	1,7	1,0	0,3
Chu kỳ thịnh hành, T1/3		7,0 s		9,0 s	11,0 s

Sự truyền sóng vào cảng

Sóng có thể truyền vào trong bến cảng theo hình thức nhiễu xạ hoặc hình thức truyền qua đập chắn sóng. Đối với hình thức sóng truyền qua, tỉ số K_T giữa chiều cao sóng truyền vào trong cảng (H_T) so với chiều cao sóng tới (H_I) là

$K_{T} = \frac{H_{T}}{H_{I}}$

Với đập chắn sóng trong cảng Akita, người ta đã xác định được giá trị sóng truyền qua như ở Bảng 2.

Bảng 2. Các giá trị ước tính của sóng truyền qua

Ch.cao sóng tới HI (m)	1,0	2,0	3,0	4,0	5,0	6,0
Ch.cao sóng truyền qua HT (m)	0,03	0,06	0,09	0,24	0,45	0,81

Ví dụ. Có nhiều công thức thực nghiệm để tính K_T; một trong những công thức đơn giản là của Kondo và Sato, K_T = 0,3 (1,5 – h_c/H_I). Hãy thử dùng công thức này để tìm H_T, biết h_c = 5,0 m là độ vượt cao của đỉnh đê chắn sóng so với mực nước trung bình. Kết quả tính được có phù hợp với con số trong Bảng 2 không?

§8. Sự phân tán năng lượng sóng theo hướng

Với hình thức nhiễu xạ, ở §6 ta đã biết cách xác định hệ số nhiễu xạ với sóng đơn hướng. Trên thực tế, sóng tới đến từ một “góc hình quạt” [phổ sóng theo hướng] thì có thể xác định một hệ số K_d tương đương:
$K_{tđ} = \sqrt{\frac{\sum_{}^{}K_{j}^{2}D_{j}}{\sum_{}^{}D_{j}}}$

Ở đây, chỉ số j ứng với các hướng sóng khác nhau. Còn D là trọng số theo năng lượng ứng với hướng sóng j cụ thể. Goda (2000) tính toán sơ bộ và chỉ ra một dạng phân phối năng lượng trong điều kiện nước sâu như ở Bảng 3.

Bảng 3. Giá trị tiêu biểu của phân bố năng lượng sóng theo hướng

Loại sóng		Dj		D (tổng hợp)
	–45°	0°	+45°	(–90°, +90°)
Sóng gió nội vùng	0,26	0,48	0,26	1,00
Sóng lừng	0,06	0,88	0,06	1,00

Ví dụ: Tính K_tđ cho trường hợp Hình 12, với 3 hướng sóng đến và phân bố năng lượng {16%, 48%, 16%}:

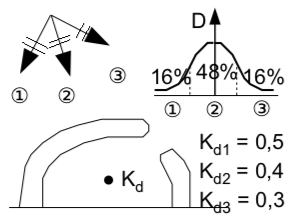
Hình 12 Bài tập tính hệ số nhiễu xạ tương đương xét đến sự phân bổ năng lượng theo hướng

Lưu ý rằng, khi sóng truyền đến gần công trình thì sự phân phối năng lượng này sẽ khác đi so với ở nước sâu: năng lượng sẽ được tập trung hơn. Hay độ phân tán của phổ năng lượng hẹp lại. Điều đó thể hiện trên biểu đồ Hình 13. Chẳng hạn, ở độ sâu h với h/L₀ = 0,1 thì tham số đặc trưng cho độ tập trung s_max, đã tăng lên thành 30 chứ không phải 10 như ở nước sâu, đối với sóng gió.

Hình 13: Độ tập trung năng lượng theo hướng ở các độ sâu nước khác nhau.

Do đó tại trước công trình (h/L_o = 0,1) thì với sóng gió như cách chia {–45°, 0°, +45°}, thì D_j = {0,16; 0,68; 0,16}. Còn với sóng lừng thì độ tập trung rất cao, D_j = {0,02; 0,96; 0,02}.

Nhiễu xạ sóng

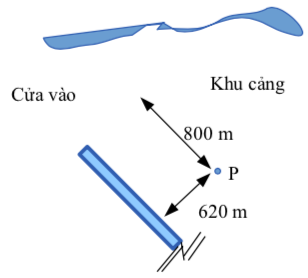
Hình 14. Vị trí điểm tính toán trong cảng

Xét hiện tượng nhiễu xạ sóng qua đầu đập chắn sóng cảng Akita (coi như đập chắn dài bán vô hạn). Tại một điểm P trong cảng (cách thân đập 620 m và lùi vào 800 m so với đầu đập chỗ cửa vào, xem Hình 14), người ta thực hiện đo đạc và xác định được các giá trị hệ số khúc xạ tính được như Bảng 4.

Bảng 4. Hệ số nhiễu xạ ứng với các hướng sóng và chu kì khác nhau

Hg′ sóng		Hệ số	nhiễu xạ
	T = 7 s	T = 9 s	T = 11 s
SW	0,101	0,116	0,130
WSW	0,277	0,290	0,303
W	0,508	0,587	0,595
WNW	0,849	0,852	0,855

Bài tập. Nếu coi đập chắn sóng có hướng Đông Nam → Tây Bắc và điểm P nêu trên, hãy kiểm tra bằng biểu đồ Hình 10 xem K_d có gần bằng giá trị trong bảng này không? (Để làm điều này, cần chỉ ra hướng sóng tới nào vuông góc với đập, và chiều dài sóng tại cửa vào cảng, nơi độ sâu h = 12 m.) Tiếp theo, hãy dùng phân bố năng lượng theo hướng (D_j) để tính ra K tương đương.

Tổng hợp chiều cao sóng

Kết quả tổng hợp sóng được trình bày ở Bảng 5, trong đó H_S, chiều cao sóng tổng hợp từ hai hình thức sóng truyền qua và nhiễu xạ, được tính theo công thức: $H_{tổng} = \sqrt{H_{T}^{2} + H_{d}^{2}}$. Có thể thấy, nói chung chiều cao sóng nhiễu xạ hơn hẳn chiều cao sóng truyền qua, chỉ trừ khi sóng đến là lớn. Hơn nữa, với hướng sóng WNW gần như trùng với hướng trục đập, chiều cao sóng truyền qua đã giảm về 0.

Bảng 5. Tổng hợp chiều cao sóng trong cảng

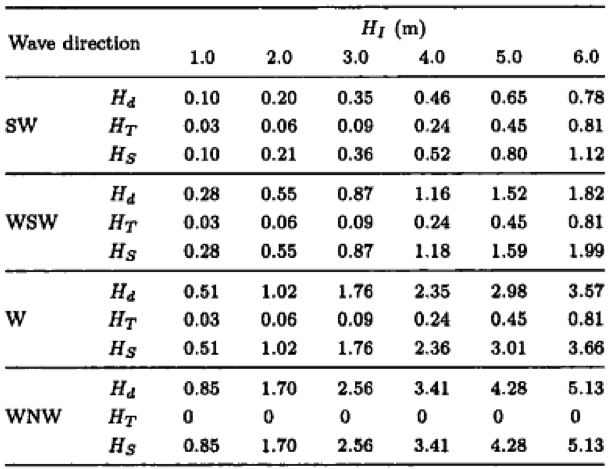
Xác suất vượt các cấp chiều cao sóng ứng với nhiều hướng

Để phục vụ cho quy hoạch cảng, cần phải đảm bảo rằng cảng phải lặng sóng trong, chẳng hạn 95%, thời gian hoạt động. Từ số liệu tần suất sóng tới và kết quả sóng tổng hợp, người ta xác lập được tần suất sóng tổng hợp cho các cấp sóng đến từ các hướng khác nhau như ở Bảng 6.

Bảng 6. Tần suất của các cấp chiều cao sóng trong cảng tương ứng với các hướng

Hướng sóng xa bờ	Chiều	cao	sóng	trong	cảng	HS
	> 0 m	> 0,5 m	> 1,0 m	> 1,5 m	> 2,0 m	> 2,5 m
SW	1,4	0	0	0	0	0
WSW	29,0	3,0	0,8	0,4	0,1	0
W	68,2	21,5	6,5	3,0	2,0	1,2
WNW	1,4	0,4	0,1	0	0	0
Tổng hợp	100,0	24,9	7,4	3,4	2,1	1,2

Như vậy, với cùng một cấp độ cao xác định thì sóng trong cảng có xác suất xảy ra nhỏ hơn nhiều so với sóng tới cùng hướng. Chẳng hạn, nếu như sóng tới từ hướng tây ở ngoài cảng với độ cao ≥ 1 m có tần suất 21,6% thì khi truyền vào trong cảng, cũng độ cao sóng này chỉ có tần suất xuất hiện là 6,5%. So sánh với Bảng 1, dễ thấy được đập chắn sóng đạt được hiệu quả giảm sóng cao.

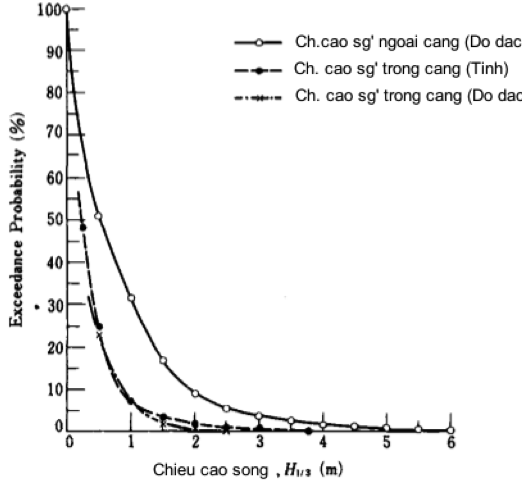
Hình 15. Xác suất các cấp chiều cao sóng truyền từ ngoài vào trong cảng

Để so sánh rõ hơn hiệu quả giảm sóng [tổng hợp tất cả các hướng] của bến cảng, người ta lập nên biểu đồ như Hình 15. Từ đó có thể nội suy ra chiều cao sóng trong cảng cũng như hiệu quả giảm sóng với cấp chiều cao bất kì. Cần nói thêm là Nhật Bản cũng tiến hành thí nghiệm đo tần suất sóng xuất hiện trong cảng; và kết quả khá phù hợp với những con số tính toán được.

§9. Nói thêm về các quá trình biến đổi sóng trong khu vực cảng

Nhiễu xạ là quá trình chi phối sóng tiến vào cửa cảng. Trong nhiều trường hợp, độ sâu đáy cảng ở gần cửa vào là không đổi, nên hệ số nhiễu xạ ở gần cửa vào hoàn toàn xác định được theo cách làm ở §6, hay §7, nếu xét thêm sóng truyền qua. Nếu phạm vi tính nhiễu xạ nếu mở rộng đến 3-4 lần chiều dài sóng trước khi độ sâu bể cảng thay đổi và cần tính khúc xạ thì tốt; còn không thì phải tính bằng mô hình số trị.

Nhiễu xạ kết hợp phản xạ trong cảng

Hiện tượng được chỉ ra như trên Hình 16. Tại điểm A có hai thành phần sóng: sóng vừa mới nhiễu xạ qua đầu đập (H_d) và sóng sau khi phản xạ (H_px). Thành phần thứ hai được ước tính bằng tích giữa chiều cao sóng lẽ ra nhiễu xạ đến điểm A’ nếu không có tường chắn, nhân với hệ số phản xạ C_r của tường này (C_r > 0).

Hiện tượng phản xạ nhiều lần trong cảng, vốn tạo nên một trường sóng “đan chéo” (Hình 17-trên) có thể gây ra khó khăn đối với tàu neo đậu hay chuyển động. Có thể phòng tránh sóng phản xạ bằng cách đặt các cấu kiện nhám vào đoạn bờ cảng dự kiến sẽ đón sóng (Hình 17-dưới), cũng như bố trí cách vách ngăn và khu trú. Chú ý rằng phản xạ có thể xuất hiện ngay sau lưng đập chắn sóng tùy theo hướng luồng vào cảng.

Hình 16. Hiện tượng phản xạ của sóng trong cảng sau đi đã nhiễu xạ qua đầu đập phá sóng.

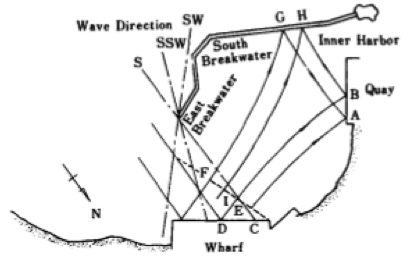
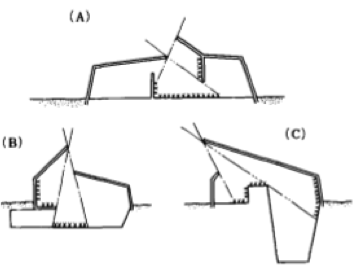
Hình 17. Phản xạ nhiều lần trong cảng (hình trên). Vị trí cần phải triệt tiêu phản xạ sóng (được đánh dấu x, hình dưới).

§10. Dao động nước trong cảng

Những dao động này là sóng đứng với chu kì từ 30 s đến 10 phút. Thường biên độ dao động theo phương đứng là nhỏ, và dao động phương ngang chiếm ưu thế. Vận tốc của dao động theo phương ngang được xác định bởi: $V_{dđ} = \frac{H_{đứng}}{2}\sqrt{\frac{g}{h}} \qquad (10.1)$

Với H_đứng là chiều cao sóng đứng (lưu ý rằng chiều cao sóng đứng gấp đôi chiều cao sóng truyền từ ngoài biển vào).

Tần số dao động riêng của bến cảng phụ thuộc vào kích thước hình học của bến cảng đó. Xét trường hợp rất đơn giản, bến cảng có dạng kéo dài ăn sâu vào trong đất liền, chiều rộng bể cảng w_B rất nhỏ so với chiều dài ℓ_B (Hình 18 - trái). Điều kiện hình thành sóng đứng có một bụng tại mặt bến và một nút tại cửa vào cảng là: ℓ_B phải bằng một số lẻ lần của phần tư chiều dài sóng nước nông: ℓ_B = (2n + 1) (¼$\sqrt{gh}T$).

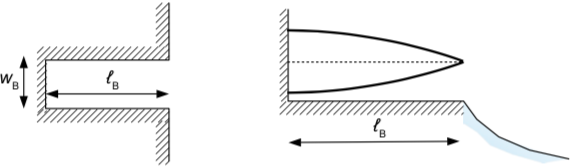
Hình 18. Cộng hưởng trong một cảng hẹp: mặt bằng (trái). Mặt đứng (phải)

Vậy chu kì dao động tự nhiên (ứng với T trong công thức trên) là
$T_{n} = \frac{4l_{B}}{\left( 2n + 1 \right)\sqrt{gh}} \qquad (10.2)$

Chu kì cơ bản ứng với n = 0, sóng đứng dạng này còn được gọi là mốt Helmholtz. Các chu kì khác sẽ có giá trị bằng 1/3, 1/5, 1/7… lần chu kì cơ bản này.

Khi tần số dao động gần bằng với tần số riêng của bến cảng thì sẽ gây ra hiện tượng cộng hưởng khiến cho biên độ dao động tăng mạnh và có thể làm đứt dây neo, hư hại tấm chắn ở bến đậu, ảnh hưởng đến quá trình bốc dỡ hàng hóa. Thực tế là các sóng triều với chu kì T_triều >> T_n không có khả năng gây cộng hưởng; một số sóng có chu kì ngắn hơn như sóng thần (tsunami), sóng do chênh lệch khí áp… có thể gây ra cộng hưởng.

Đối với các bến cảng có chiều rộng w_B đáng kể so với ℓ_B thì vẫn có thể hình thành sóng đứng như Hình 18 song chu kì tính theo công thức (10.2) không còn chính xác nữa.

Mặt khác, trường hợp này còn có thể hình thành nên sóng đứng theo hướng ngang cảng. Điểm khác biệt so với trường hợp trước là hình thành 2 bụng sóng ở hai phía thành bể cảng (Hình 19).

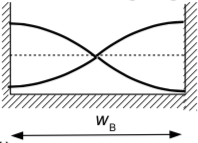
Hình 19. Cộng hưởng theo hướng ngang cảng

Chu kì dao động tự nhiên với loại cộng hưởng này là:

$T_{n} = \frac{2\ell_{B}}{n\sqrt{gh}}$

Chú ý trong trường hợp cộng hưởng có 2 đầu kín (đều là bụng sóng) này thì mốt thấp nhất là n = 1.

Hình 19b. Chu kì dao động tự nhiên (surge & sway) của các tàu với tải trọng khác nhau

§11. Kích thước cơ bản của tàu

Với nội dung trong §11, sinh viên cần tham khảo Bài giảng Vận tải thủy.

• Chiều dài L (có thể phân biệt cụ thể hơn: LOA và LBP hay L_pp). LOA (chiều dài lớn nhất) có ý nghĩa quan trọng để xác định kích thước bến bãi, luồng cảng, bố trí dây neo, tính toán tải trọng gió tác dụng lên tàu. LBP (chiều dài hai trụ) coi như bằng khoảng cách dài giữa hai mép nước mũi-đuôi tàu và thường bằng 95% của LOA với các tàu lớn. LBP quan trọng để tính ổn định dưới tải trọng sóng - dòng chảy. Một kích thước quan trọng khác là chiều dài khúc thân song song (LPM, length of parallel mid-body), mà sau đây ta dùng để tính bố trí khoảng cách giữa hai tấm chắn.
• Bề rộng B
• Mớn nước (draught/draft) D
• Mạn khô ổn định (freeboard), F, có thể ảnh hưởng đến độ ổn định nghiêng nhưng không ảnh hưởng quá trình thủy động lực.

Các đại lượng dẫn xuất

• Thể tích chiếm nước: ∇ = C_B × LOA × B × D
  trong đó C_B: hệ số béo (0,6 → 0,9). Những tàu nhỏ thì cũng có C_B nhỏ hơn so với những tàu lớn. Hệ số béo cụ thể của một số loại tàu như sau:

• Tàu bồn chở hóa chất 0,73 – 0,82

• Tàu bồn rất lớn 0,82 – 0,84

• Tàu contennơ 0,63 – 0,71

• Tàu chở hàng thường 0,71 – 0,77

• RO/RO 0,71 – 0,80

• Phà 0,57 – 0,63

(Lượng chiếm nước = ∇ × khối lượng riêng nước biển (1,025 T/m³).

Chú ý rằng lượng chiếm nước cũng như mớn nước đều thay đổi với cảng cửa sông theo tỉ lệ γ / γ₀ trong đó γ₀ là dung trọng nước cửa sông.

• Tải trọng tàu: Có ba loại tải trọng. Tải trọng khô (dead weight tonnage, DWT) của tàu gồm trọng lượng nhiên liệu, hàng hóa, đoàn thủy thủ cùng lương thực, vật dụng … Tải trọng nhẹ (light-weight tonnage, LWT) chính là trọng lượng phần sắt thép cấu trúc nên tàu. Tải trọng chiếm nước (displacement tonnage, DT) chính là tổng hai loại tải trọng nêu trên.

DT = DWT + LWT

Đơn vị đo tải trọng thường là tấn. Lưu ý rằng các thuật ngữ gross/net register ton (tấn đăng ký), vốn dùng để chỉ kích cỡ và năng lực chuyên chở của tàu, thực ra không phải trọng lượng mà là một đơn vị thể tích bằng 100 ft³ hay ≈ 2,83 m³.

• Dung tích của tàu côngtennơ được đo bằng TEU, vốn xấp xỉ thể tích một côngtennơ dài 6,1 m; các chiều cao và rộng đều bằng 2,44 m. Các tàu chở xăng và khí đốt (LPG, LNG) thì dùng thể tích (m³) của lượng nhiên liệu chuyên chở.

§12. Chuyển động cơ bản của tàu

Chuyển động của tàu như một vật rắn có 6 bậc tự do (Hình 19c):

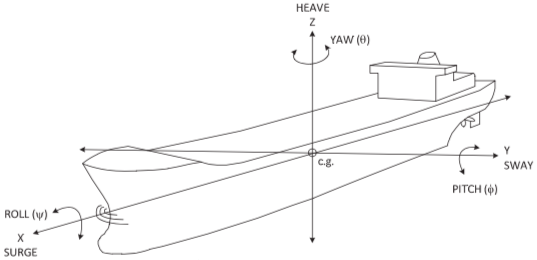
Hình 19c. Các dạng chuyển động cơ bản của tàu (Gaythwaite 2014)

• 3 tịnh tiến theo 3 phương: tiến-lùi, dịch ngang và chìm-nổi;
• 3 quay: xoay đứng, xoay ngang, xoay dọc

Hiện tượng chìm đều, “squat”: Khi tàu chuyển động trong vùng có độ sâu bị hạn chế hoặc trong kênh hẹp, lớp nước mỏng dưới đáy tàu (hoặc lớp nước sát thành kênh) sẽ được chuyển động tương đối nhanh, gần bằng vận tốc chạy tàu. Theo định luật Becnuli, vùng chất lỏng chuyển động nhanh sẽ có áp suất thấp nên sự mất cân bằng áp suất sẽ khiến tàu bị chìm xuống.

Squat có thể được tính theo một số công thức kinh nghiệm như công thức Barrass, công thức ICORELS (sau đó được đưa vào tiêu chuẩn PIANC). Ở đây ta xét công thức ICORELS:

$SQUAT = \frac{2,4}{L_{\text{BP}}^{2}}\nabla\frac{F^{2}}{\sqrt{1 - F^{2}}}$ (đơn vị SQUAT theo công thức này là mét)

trong đó F là số Froude (Frút), $F = \frac{V_{s}}{\sqrt{gh}}$ (không thứ nguyên). Ảnh hưởng của độ sâu thể hiện qua số Frút này.

Trong trường hợp tàu chuyển động trong kênh thì, theo Huuska & Guliev tác động thu hẹp dòng chảy thể hiện qua một hệ số K_S phụ thuộc vào tỉ số giữa tiết diện ngang của tàu và mặt cắt ngang của kênh. Trường hợp kênh không giới hạn thì K_S = 1 và ta có công thức tiêu chuẩn của ICORELS.

Ngoài ra do tác động của sóng, ở tàu còn hiện tượng chìm không đều giữa mũi và đuôi do sóng, gọi là “trim”. Hiện nay phương pháp để tính trim chủ yếu là dựa vào các thí nghiệm vật lý.

§13. Các lực môi trường tác dụng lên tàu

Sau đây ta sẽ xét các lực do gió, do sóng và do dòng chảy tác động lên tàu, được gọi chung là lực “môi trường”. Một lực được phân tích theo hai hướng: dọc trục tàu và hướng ngang tàu. Trong các công thức dưới đây, với dung trọng nước γ tính theo T/m³ thì lực F tính theo tấn (chú ý đơn vị lực: 1 T = 1000 kG = 9810 N).

Nguyên tắc chung khi tính lực tác dụng lên tàu là áp dụng công thức cơ bản trong cơ học lưu chất: F = C_D ρ A U², trong đó C_D là hệ số cản hình dạng (càng nhỏ đối với vật thể thuôn dài, ≈ 1 với tiết diện lăng trụ), A là tiết diện vật chắn dòng chảy còn U là vận tốc dòng chảy. Tàu có thể được coi là khối hộp chữ nhật có đáy phẳng, nằm ngang. Khi dòng chảy xiên góc β so với trục tàu thì tiết diện của tàu chắn dòng chảy (Hình 20) là:

A = (L sinβ + B cosβ) D

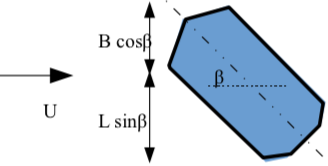
Hình 20. Minh họa tiết diện chắn dòng chảy của tàu (chiều sâu bằng D)

Lực do sóng (theo tiêu chuẩn ROM 0.2-90, Tây Ban Nha) hai thành phần lực này là:

F_{ngang, sóng} = C_Ds × C_hs × γ × H_s² × L’ × sinβ
F_{dọc, sóng} = C_Ds × C_hs × γ × H_s² × L’ × cosβ

trong đó: β là góc giữa hướng sóng và hướng trục tàu

L’ = L_BP sinβ + B cosβ, là hình chiếu của chiều dài tàu theo hướng sóng tới.

C_Ds là hệ số phụ thuộc vào tương quan giữa mớn nước D với chiều dài sóng L (tra Hình 21-trái). C_hs là hệ số phụ thuộc tương quan giữa độ sâu h với L (tra Hình 21-phải). γ là dung trọng của nước = 1,03 T/m³ với nước biển.

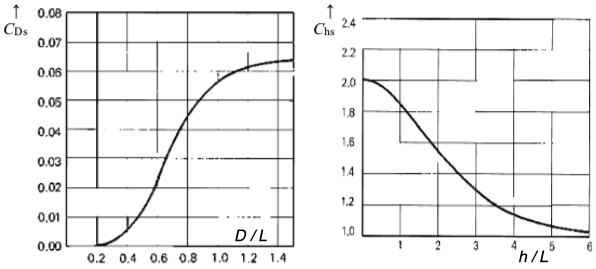
Hình 21. Đồ thị xác định các hệ số C_Ds và C_hs

Lực do gió (theo tiêu chuẩn ROM) Cũng như lực do gió, dạng chung là F tỉ lệ với bình phương lưu tốc (của dòng nước hay luồng gió).

• hợp lực tác dụng lên tàu (tính theo kN):

$R = C_{V} \times \left( A_{t}\cos^{2}\beta + A_{d}\sin^{2}\beta \right) \times \frac{U^{2}}{1600}$

với C_v là hệ số hình dạng tàu, có thể lấy bằng 1,3. A_d và A_t lần lượt là hình chiếu tàu (phần hứng gió) theo mặt bên (dài), và theo mặt trước. Theo viện nghiên cứu hải cảng Nhật Bản thì diện tích này có dạng hàm số: A_t,d [m²] = k (DWT)ⁿ với DWT tính bằng tấn còn k, n là các hệ số cho ở Bảng dưới đây.

Bảng: Các giá trị k và n để tính diện tích hình chiếu chắn gió

β là góc giữa hướng gió và hướng trục tàu, U là vận tốc gió thiết kế ở độ cao 10 m, trong thời khoảng đủ dài để thắng được quán tính của tàu. Khuyến nghị lấy thời khoảng 1 phút với tàu có chiều dài ≥ 25 m, và 15 s với tàu có chiều dài < 25 m. Riêng những tàu cao thì cần xét đến phân bố vận tốc gió theo phương thẳng đứng. Phân bố này có dạng hàm mũ: U(z) = U₁₀ (z/10)ⁿ , trong đó hệ số kinh nghiệm n ~ 1/9 → 1/8 với vùng biển gần bờ.

• hướng của hợp lực so với trục tàu được xác định bởi góc φ sao cho:

tanφ = tan β × A_d / A_t

• các thành phần lực hướng ngang và hướng dọc trục tàu sẽ là

F_ngang,gió = R sinφ   và   F_dọc,gió = R cosφ

Câu hỏi. Hãy chỉ ra rằng vec-tơ hợp lực không cùng hướng với hướng gió, cụ thể vec-tơ hợp lực nằm giữa hướng sóng tới và hướng trục tàu. (Tận dụng điều này mà các thuyền buồm nhỏ có thể đi ngược chiều gió. Gợi ý: căn cứ vào công thức tanφ = tan β × A_d / A_t .)

Ví dụ tính toán. Tàu chở dầu 200 000 dwt, có LOA = 350 m, LBP = 346 m, B = 56,2 m. Trong điều kiện không tải (ba-lát), diện tích hình chiếu cạnh dài là A_d = 6930 m², diện tích hình chiếu trước/sau là A_t = 1730 m².

a) Hãy tính hợp lực tác dụng lên tàu theo các điều kiện gió lần lượt là U = 10 m/s, 15 m/s, 20 m/s trong hai trường hợp: gió thổi xuôi dọc tàu (β = 0) và ngang tàu (β = 90°).
b) Tính lại như câu trên với trường hợp tàu chở đầy hàng với A_d = 4300 m², và A_t = 1210 m².

Lực do dòng chảy (tiêu chuẩn ROM): gồm hai yếu tố: gây bởi áp suất lên mặt trực diện hứng dòng chảy và do lực cản phương tiếp tuyến với vỏ tàu.

• yếu tố gây bởi áp suất:
  F_ngang,aps = C_ng × γ × A_d,dc × sinβ × V²/2g
  F_dọc,aps = ±C_dọc × γ × A_t,dc × sinβ × V²/2g

với C_ng: hệ số cản ngang, phụ thuộc độ sâu tương đối h/D tra hình 22; A_d,dc tương đương với A_d nhưng là phần dưới nước, A_t,dc tương đương với A_t nhưng là phần dưới nước, cụ thể:

A_d,dc = L_BP × D và A_t,dc = B × D

(chú ý rằng áp lực ngang ứng với hình chiếu diện tích theo phương dọc)

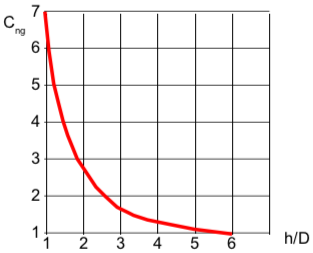
Hình 22. Đồ thị xác định hệ số hình dạng tàu phục vụ tính lực dòng chảy tác dụng ngang tàu.

C_dọc là hệ số cản theo hướng dọc trục tàu, phụ thuộc vào hình dạng mũi tàu, = 0,6 với mũi uốn cong thông dụng; V là lưu tốc dòng chảy, tính theo m/s, ở độ sâu D/2 đo trong thời khoảng 1 phút.

• yếu tố gây bởi lực cản tiếp tuyến:
  F_ngang,cản = C_cản × γ × A^*_t,dc × sin²β × V²/2g
  F_dọc,cản = C_cản × γ × A^*_d,dc × cos²β × V²/2g

với C_cản = hệ số ma sát vỏ tàu, = 0,001 với tàu mới và 0,004 với tàu đã sử dụng. A^* là các diện tích ướt trên vỏ tàu xuất hiện lực cản tiếp tuyến; (chú ý rằng lực cản dọc sẽ ứng với A^*_d): Hình minh họa các diện tích A* này

A^*_t,dc = (L_BP + 2D) × B   và   A^*_d,dc = (B + 2D) × L_BP

Ví dụ. Vẫn lấy kích thước tàu như trên, bổ sung D = 20,4 m. Hãy tính lực cản do dòng chảy trong các trường hợp h/D = 1,1; 1,5; 2,0 (cũng xét dòng chảy dọc tàu (β = 0) và ngang tàu (β = 90°).

§14. Khả năng điều động tàu

Sau khi xét đến chuyển động của tàu như một vật thể với 6 bậc tự do, lẽ tự nhiên ta muốn tìm hiểu khả năng di chuyển của tàu trên thực tế. Tuy nhiên đây là vấn đề phức tạp, và thường không thể trình bày bằng những công thức phù hợp cho thao tác tính toán thủ công. Do đó, tính toán điều động tàu là chủ đề vượt khỏi khuôn khổ tập bài giảng này. Thay vào đó, ta chỉ lưu ý một số điều cơ bản nhất. Chẳng hạn, tàu chạy trong luồng không thể theo một đường thẳng, mà chuyển động thực tế của tàu trong kênh là hình sin, do những tác động do sóng, gió và dòng chảy hướng vào mạn tàu.

Khả năng rẽ của tàu cũng bị giới hạn bởi quán tính và độ hạn chế góc bẻ bánh lái. Tàu vào cảng cần phải quay …để cập bến và đi trở ra. Thao tác quay tàu thường đòi hỏi một phạm vi điều động nhất định, tùy thuộc vào loại tàu. Chẳng hạn, với các tàu contenơ, loại tàu khó điều động nhất, đường kính quay tàu lên tới (6 → 8)L, với các tàu lớn chở dàu hoặc hàng khô rời, đường kính này là (3 → 4)L; với các tàu chở LNG hoặc chở hàng thường, (2 → 2,5)L. Đây là trường hợp có tàu lai dắt (tug boats); nếu không có sự trợ giúp này thì đường kính quay tàu sẽ tăng lên. Chẳng hạn với hàng thường, nếu như với tàu lai dắt, đường kính tối thiểu = 2L thì khi không có lai dắt, đường kính này là 4L.

Khi tiến vào cửa cảng để đảm bảo an toàn cho tàu đi lại, thường chọn chiều dài cửa cảng = (0,7 → 1,0)L. Cửa cảng cũng không quá rộng, tránh nhiều sóng truyền vào trong. Quá trình tiến vào cảng của tàu như thể hiện qua ví dụ hình 22b.

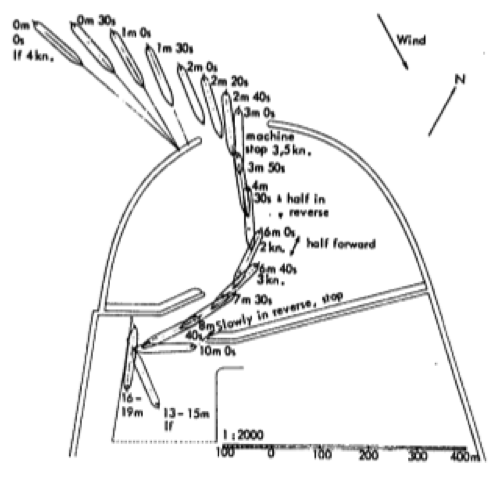
Hình 22b: Đường di chuyển của tàu cập bến tại Cảng Hanstholm, Đan Mạch (Svendsen, 1968)

Khoảng cách dừng tàu, s: Khoảng cách này phụ thuộc vào các yếu tố như tốc độ tàu, thể tích chiếm nước và hình dạng mũi tàu, và tỉ số công suất ∇/P (trong đó P là công suất tàu tính bằng mã lực). Với các tàu không tải thì khoảng cách này có thể bằng 3L → 5L; với các tàu chở đầy hàng thì khoảng cách này có thể từ 7L → 8L. Có thể dựa vào biểu đồ trên Hình 23 (Giáo trình Vận tải thủy).

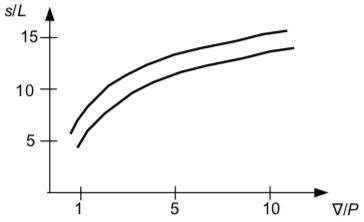
Hình 23. Biểu đồ liên hệ khoảng cách dừng tàu với thể tích chiếm nước

§15. Kích thước bể cảng

Yêu cầu về độ sâu của bến: Cũng như theo quan điểm của thiết kế tuyến luồng, mặc dù trong những trường hợp đặc biệt có thành phần với giá trị nhỏ, bỏ qua được. Chẳng hạn, nếu không phải cảng cửa sông thì ta không tính thêm độ chìm do chênh lệnh mật độ nước. Hay nếu như khu vực bến là tương đối nhỏ (so với toàn bộ phạm vi cảng và lân cận) thì việc đo sâu có thể tin cậy và không xét đến sai số đo sâu. Hình 24 biểu diễn các độ sâu hợp thành độ sâu yêu cầu đối với bến. Độ sâu nước này được tính từ mực nước triều thiên văn thấp nhất xuống đáy biển.

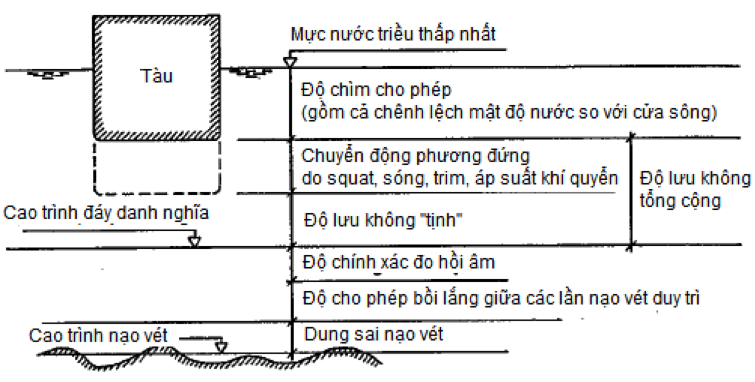
Hình 24. Yêu cầu độ sâu của bến (Thoresen)

Chiều dài của bến đậu được xác định sao cho đủ chỗ cho cả chiều dài tàu cập bến, đồng thời chừa ra khoảng cách giữa các tàu (cỡ 15 m với tàu chở hàng tổng hợp, có tàu lai dắt; hoặc nếu với trường hợp khó điều động hơn thì cỡ 30 m). Cụ thể hơn, với bến đậu n tàu nối đuôi nhau, chiều dài bến được xác định bởi:

L_Q = 1,1 n (LOA + 15) + 15

Thoresen khuyến nghị một quy tắc đơn giản: khi hai tàu đỗ nối tiếp nhau thì khoảng cách giữa chúng lấy bằng 0,1 lần chiều dài của tàu lớn hơn. Còn về yêu cầu bề rộng, bến phải đủ chỗ chứa một số con tàu rộng nhất (B_max) và thêm một khoảng trống phục vụ điều động tàu. Một ví dụ cho cách bố trí bến tàu được minh họa trên Hình 25. Lưu ý khoảng cách từ mũi tàu đến bờ: nếu bờ có dạng mái dốc như trường hợp con tàu ngoài cùng phía bên trái thì khoảng cách an toàn (0,15L) phải được tính từ mũi tàu đến chân mái dốc chứ không phải đến mép nước.

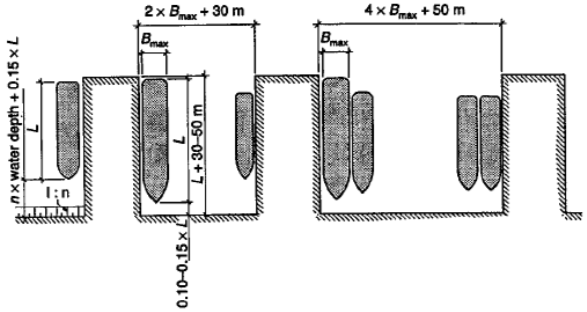
Hình 25. Bố trí kích thước mặt bằng của bến (Thoresen)

Số bến tàu, n_b, trong cảng được xác định qua việc phân tích để cân đối giữa chi phí xây dựng vận hành bến, và chi phí cho thời gian chờ tàu. Hoặc với tàu chở hàng thường có thể xác định qua chỉ số chiếm chỗ bến tàu, đối với tàu chở hàng thường, như sẽ trình bày sau đây.

• Thực nghiệm cho thấy sự cập bến của tàu theo phân bố Poisson: xác suất P(n) để n tàu cập bến trong một thời khoảng cho trước—thường là 1 ngày—thì bằng: P(n) = N_e e^–N / n!, trong đó N là số trung bình các tàu cập bến mỗi ngày, xét về lâu dài. Phát biểu trên tương đương với phân bố thời khoảng t_CB giữa hai lần cập bến liên tiếp thì tuân theo luật phân bố lũy thừa âm: P_cb(t) = exp(–t_cb / t_cb), trong đó t_cb là trung bình các thời khoảng này xét về lâu dài. Mặt khác, theo số liệu thì khoảng thời gian phục vụ (v.d. bốc dỡ…) của tàu trong bến, t_pv, lại tuân theo phân bố Erlang với tham số k = 2: P_pv(t) = (2t_pv/t_pv) exp(–2t_pv/t_pv).

• Mức độ chiếm chỗ ở bến được biểu diễn bởi phần trăm thời gian mà các bến bị tàu chiếm chỗ. Mức độ này phụ thuộc vào dạng phân bố cập bến, thời gian phục vụ, và số lượng bến (n_b). Chỉ số chiếm chỗ là k_o = N × t_pv / n_b.

  Chỉ số tắc nghẽn k’_o là tỉ số phần trăm giữa thời gian chờ và thời gian phục vụ.

• Số lượng bến có thể xác định xấp xỉ theo lượng hàng hóa thông qua, Q, theo đơn vị 100000 T/năm như công thức: n_b ≈ Q / k_o.

Hình 26. Minh họa thời gian cập bến và thời gian phục vụ của 3 tàu lần lượt cập vào một bến cảng.

Việc tính toán các chỉ số chiếm chỗ và tắc nghẽn phải thông qua mô phỏng ngẫu nhiên và là nội dung quan trọng trong lĩnh vực lý thuyết hàng đợi. Do tính toán này rất phức tạp nên người ta đã tính sẵn và lập ra bảng tra cho tiện. Chẳng hạn, đối với tàu chở hàng thường thì tàu đến với luật phân bố Poisson (hay còn gọi là một quá trình Markov), và thời gian phục vụ theo phân bố Erlang bậc 2 với n_b bến thì ta có Bảng 7. (Kí hiệu M/E2/n_b là theo lý thuyết hàng đợi.)

Bảng 7: Chỉ số tắc nghẽn với hàng đợi theo luật M/E2/n_b

k′o ↘	Số bến,	nb →
ko ↓	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0,10	0,08	0,01	0	0	0	0	0	0	0	0	0	0	0	0	0
0,15	0,13	0,02	0	0	0	0	0	0	0	0	0	0	0	0	0
0,20	0,19	0,03	0,01	0	0	0	0	0	0	0	0	0	0	0	0
0,25	0,25	0,05	0,02	0	0	0	0	0	0	0	0	0	0	0	0
0,30	0,32	0,08	0,03	0,01	0	0	0	0	0	0	0	0	0	0	0
0,35	0,40	0,11	0,04	0,02	0,01	0	0	0	0	0	0	0	0	0	0
0,4	0,50	0,15	0,06	0,03	0,02	0,01	0,01	0	0	0	0	0	0	0	0
0,45	0,60	0,20	0,08	0,05	0,03	0,02	0,01	0	0	0	0	0	0	0	0
0,50	0,75	0,26	0,12	0,07	0,04	0,03	0,02	0,01	0,01	0,01	0	0	0	0	0
0,55	0,91	0,33	0,16	0,10	0,06	0,04	0,03	0,02	0,02	0,01	0,01	0,01	0	0	0
0,60	1,13	0,43	0,23	0,14	0,09	0,06	0,05	0,03	0,03	0,02	0,02	0,01	0,01	0,01	0,01
0,65	1,38	0,55	0,30	0,19	0,12	0,09	0,07	0,05	0,04	0,03	0,03	0,02	0,02	0,02	0,02
0,70	1,75	0,73	0,42	0,27	0,19	0,14	0,11	0,09	0,07	0,06	0,05	0,04	0,03	0,03	0,03
0,75	2,22	0,96	0,59	0,39	0,28	0,21	0,17	0,14	0,12	0,10	0,08	0,07	0,06	0,05	0,05
0,80	3,00	1,34	0,82	0,57	0,42	0,33	0,27	0,22	0,18	0,16	0,13	0,11	0,10	0,09	0,08
0,85	4,50	2,00	1,34	0,90	0,70	0,54	0,46	0,39	0,34	0,30	0,26	0,23	0,20	0,16	0,10
0,90	6,75	3,14	2,01	1,45	1,12	0,91	0,76	0,65	0,56	0,50	0,45	0,40	0,36	0,33	0,30

Với hàng container, thì tàu đến tuân theo phân bố Erlang bậc 2 và lý thuyết hàng đợi theo luật E2/E2/n_b cho ta kết quả khác đi (Bảng 8).

Bảng 8: Chỉ số tắc nghẽn với hàng đợi theo luật E2/E2/n_b

k′o ↘	Số bến,	nb →
ko ↓	1	2	3	4	5	6	7	8
0,10	0,02	0	0	0	0	0	0	0
0,15	0,03	0,01	0	0	0	0	0	0
0,20	0,06	0,01	0	0	0	0	0	0
0,25	0,09	0,02	0,01	0	0	0	0	0
0,30	0,13	0,02	0,01	0	0	0	0	0
0,35	0,17	0,03	0,02	0,01	0	0	0	0
0,40	0,24	0,06	0,02	0,01	0	0	0	0
0,45	0,30	0,09	0,04	0,02	0,01	0,01	0	0
0,50	0,39	0,12	0,05	0,03	0,01	0,01	0,01	0
0,55	0,49	0,16	0,07	0,04	0,02	0,02	0,01	0,01
0,60	0,63	0,22	0,11	0,06	0,04	0,03	0,02	0,01
0,65	0,80	0,30	0,16	0,09	0,06	0,05	0,03	0,02
0,70	1,04	0,41	0,23	0,14	0,10	0,07	0,05	0,04
0,75	1,38	0,58	0,32	0,21	0,14	0,11	0,08	0,07
0,80	1,87	1,83	0,46	0,33	0,23	0,19	0,14	0,12
0,85	2,80	1,30	1,75	0,55	0,39	0,34	0,26	0,22
0,90	4,36	2,00	1,20	0,92	0,65	0,57	0,44	0,40

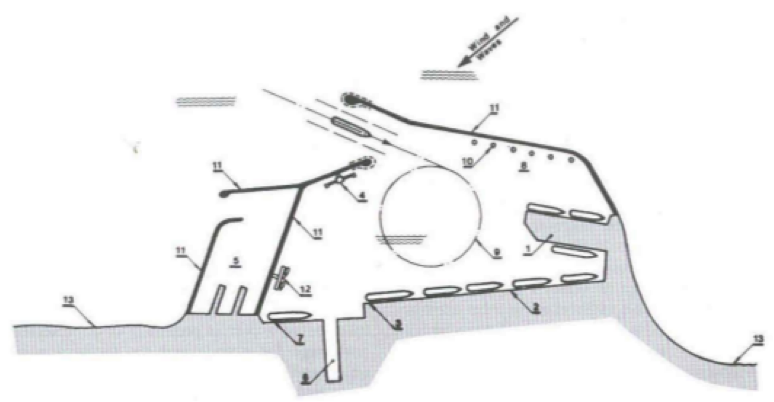
Hình 27. Các thành phần của bến cảng đa mục tiêu: 1. Bến đón hàng tổng hợp; 2. bến container; 3. bến đón khách; 4. bến cấp dầu; 5. cảng cá; 6. xưởng cạn; 7. khu sửa tàu; 8. khu thả neo; 9. vùng quay trở; 10. neo rùa; 11. đập phá sóng; 12. bến tàu lai dắt; 13. đường bờ.

15. Dao động của tàu khi neo đậu

Để phân tích động lực học của tàu ta coi tàu như một vật rắn; và để đơn giản thì xét trên mặt phẳng ngang. Khi đó có ba ẩn số chuyển động của tàu (xem lại §12) là tiến thẳng (X, surge), dịch ngang (sway, Y) và quay ngang (yaw, Ψ).

Hình 27b. Các lực và chuyển động của tàu trong phân tích động lực đơn giản

Dao động của tàu khi neo bằng định luật II Newton được biểu diễn bằng PT:

$\left( m + a \right)\ddot{x} + b\dot{x} + cx = F\left( t \right)$

trong đó x là vec-tơ vị trí của tàu theo ba phương không gian, $\dot{x}$ là vận tốc còn $\ddot{x}$ là gia tốc của tàu. m là khối lượng tàu, a là khối lượng phụ thêm, b là hệ số tắt dao động còn c là hệ số hồi phục. F là vec-tơ ngoại lực do sóng, gió, dòng chảy hoặc tàu khác.

§16. Luồng tàu

Luồng tàu có thể được phân chia dựa theo mức độ quan trọng (có/không có đảm bảo độ sâu, có/không trợ giúp giao thông ngày/đêm), hay theo loại mặt cắt ngang (luồng có hạn chế, bán hạn chế, hoặc không hạn chế). Luồng thẳng gồm 1 hoặc 2 làn. Phương pháp thiết kế luồng theo các bước sau:

a) Chọn tàu thiết kế
b) Xác định điều kiện môi trường (độ sâu nước, thủy triều, dòng chảy, sóng gió) cho từng đoạn tuyến chạy của tàu.
c) Xác lập vận tốc của tàu, yêu cầu về lai dắt, điều động.
d) Ước tính độ sâu luồng
e) Ước tính yêu cầu bề rộng
f) Xác định độ dốc mái của luồng
g) Đặt tuyến luồng lên trên nền địa hình hiện có
h) Thẩm định lại kích thước luồng qua mô hình mô phỏng điều động tàu
i) Xác định yêu cầu về phương tiện trợ giúp hàng hải
j) Lập kích thước chi tiết, giá thành nạo vét, tính khả thi về kinh tế và môi trường.

Một số nguyên tắc chung uồng di chuyển phải tính đến sự quay ngang của tàu, với góc cỡ ±5°. Với luồng một làn, bề rộng đáy luồng = (3,6 → 6) B. Với luồng hai làn, bề rộng đáy luồng = (6,2 → 9) B.

Với kênh cong (> 10°), nên nắn thẳng bằng cách nạo vét bờ kênh phía trong.

Thiết kế chi tiết

Độ sâu luồng, gồm các thành phần: mớn nước D, SQUAT, chuyển động của mũi tàu (z_mũi, có thể tính qua chương trình máy tính), độ sâu lưu không, dung sai nạo vét, dung sai đo sâu, dự trữ bồi lắng giữa hai kì nạo vét liên tiếp.

Bề rộng luồng được thiết kế theo tiêu chuẩn PIANC. Do tàu chuyển động theo một đường lượn cong như hình sin nên phạm vi đường bao của hình sin này là một dải điều động cơ bản có bề rộng W_BM (basic maneuvering) từ 1,2B → 1,8B. Ngoài ra, cần dành riêng một khoảng bề rộng dự trữ ΣW_i cho các yếu tố môi trường (gió, sóng, dòng chảy, độ sâu luồng, mức độ nguy hiểm của hàng hóa …) Hai bên bờ sát luồng cần chừa ra bề rộng dự phòng (lưu không) W_Br và W_Bg. Các giá trị thích hợp cho W_BM , W_i và W_B đều được tra trong bảng của PIANC.

Công thức bề rộng cho luồng gồm 1 làn tàu và 2 làn tàu lần lượt là:

W₁ = W_BM + ΣW_i + W_Bg + W_Br
W₂ = 2(W_BM + ΣW_i) + W_P + W_Bg + W_Br

Chi tiết về các thành phần bề rộng có thể tra trong Bảng tiêu chuẩn PIANC (xem sách giáo trình Vận tải thủy).

Với đoạn luồng cong, các thông số bao gồm bán kính đoạn cong, R_cong, và bề rộng đoạn cong W_cong, cả hai đều được xác định từ biểu đồ (các hình 28 và 29).

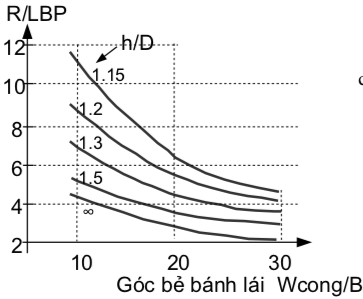
Hình 28. Liên hệ giữa bán kính cong tương đối (so với chiều dài tàu) với góc bẻ bánh lái và độ sâu nước tương đối.

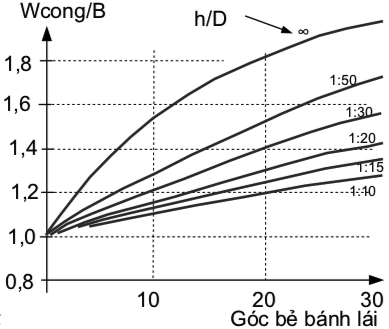
Hình 29. Liên hệ giữa chiều rộng đoạn rẽ tương đối (so với bề rộng tàu) với góc bánh lái và độ sâu tương đối

§17. Tác động của tàu lên mặt bến

Tàu tiếp cận với mặt bến theo một góc bằng ϕ nhằm giảm vận tốc về 0 (xem Hình 30). Tại điểm O có đặt một tấm chắn đàn hồi để giảm lực va đập và tàu quay xung quanh điểm tựa này. Sau đó, để phần đuôi tàu không bị va đập vào mặt bến thì cần phải có một tấm chắn thứ hai; tấm này cách tấm trước một đoạn bằng LPM (xem lại §11). Khoảng cách này phải không quá lớn để phần vỏ thân tàu vẫn cách khỏi mặt bến. Kinh nghiệm chọn LPM ≈ 0,7 LOA.

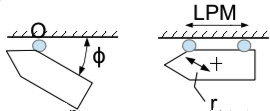
Hình 30. Sơ đồ quá trình cập bến của tàu

Tác động của tàu lên mặt bến được đánh giá qua động năng va chạm. Về bản chất vật lý, động năng tỉ lệ với một nửa tích (½mV²) nhưng trong trường hợp áp dụng với va chạm của tàu lên bến, ta cần giới thiệu một vài nhân tố hiệu chỉnh thể hiện trong công thức sau:

E = C_H × C_E × C_C × C_S × ½M_tkV².

Trong đó các kí hiệu C biểu thị các hệ số điều chỉnh, cụ thể gồm có:

Nhân tố khối lượng thêm (added mass), hay khối lượng thủy động: C_H > 1, nhân tố này tồn tại do một tính chất cơ bản của thủy động lực học: một vật rắn đặc chuyển động trong chất lỏng thì sẽ kéo theo một lớp chất lỏng quanh đó chuyển động với cùng vận tốc, từ đó mà có quán tính cao hơn, hay nói cách khác, có “khối lượng phụ thêm”.

Hệ số C_H có thể được tính theo một số công thức:

C_H = 1,0 + 2,0 D/B (Vasco Costa 1964)
C_H = 1 + πD / 2C_BB (Ueda 1981)

Ngoài ra, có thể áp dụng quy tắc kinh nghiệm: Với nước sâu tối thiểu 1,5D thì C_H = 1,5 và với nước rất nông, cỡ 1,1D thì C_H = 1,8. Mặt khác Saurin (1963), qua việc lập mô hình thu nhỏ và quan sát thực tế, đã đều xuất giá trị trung bình = 1,3 và giá trị an toàn = 1,8 cho C_H.

Nhân tố lệch tâm, gắn liền với năng lượng tiêu hao do chuyển động quay trong quá trình đỗ, quanh điểm chạm gần phía mũi hoặc đuôi tàu,

$C_{E} = \frac{I_{q}^{2} + r^{2}\cos^{2}\varphi}{I_{q}^{2} + r^{2}}$

trong đó I_q là bán kính quán tính của tàu, lấy bằng 0,2L → 0,5L; r là khoảng cách giữa điểm tiếp xúc đến khối tâm của tàu; ϕ là góc giữa đường bến với trục tàu.

Khi ϕ ↗ 90°, năng lượng va chạm giảm. Với ϕ nhỏ (0 → 15°, như khi không có tàu lai dắt), thường r = 0,25L → 0,35L. Khi đó C_E = 0,5 → 0,6 với fender liền tấm, và = 0,7 → 0,8 với các cọc rời hay breasting dolphin.

Với ϕ = 0° thì năng lượng va chạm lớn, song phần mặt tiếp xúc va chạm cũng lớn hơn.

Nhân tố hiệu ứng giam nước (cushion effect), CC, phát sinh khi xét đến phần nước bị ép giữa mặt bến dạng tấm liền với thân tàu khi mạn tàu áp sát thân bến. Thường lấy C_C = 0,8 → 1,0.

Nhân tố va chạm mềm, C_S, là tỉ số giữa độ đàn hồi của vỏ tàu với độ đàn hồi của tấm đỡ. Một phần động năng sẽ được hấp thụ qua biến dạng đàn hồi của vỏ tàu. Thường lấy C_S = 0,9 → 1,0. Với tàu nhỏ, lấy bằng 1,0.

Hiển nhiên, năng lượng va chạm gần như tỉ lệ với khối lượng thiết kế Mtk của tàu và với bình phương của vận tốc tới gần, V. Đây là thành phần vận tốc vuông góc mặt bến. Quy định về tốc độ V tùy thuộc chủ yếu vào tải trọng tàu; ngoài ra còn phụ thuộc vào các điều kiện thời tiết và khả năng điều động tàu (Hình 31).

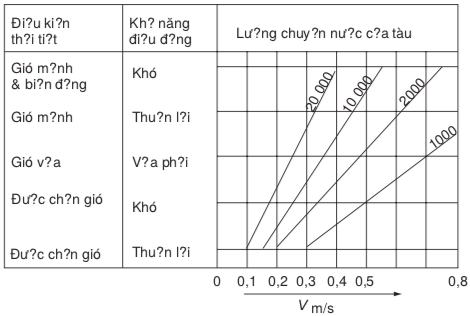
Hình 31. Vận tốc tới gần thích hợp đối với các tàu có tải trọng khác nhau
trong điều kiện định tính về thời tiết và khả năng điều động tàu

Bài tập.

1) Liệu hệ số C_E sẽ tăng hay giảm khi góc cập bến ϕ tăng; như vậy sẽ có tác động nguy hiểm đến bến không?

2) Độ nhạy của C_E theo ϕ như thế nào? Hãy xét trường hợp ϕ biến đổi từ 10° đến 30°. Để tính độ nhạy, ta xác định tỉ số (ΔC_E/C_E) / (Δϕ /ϕ). độ nhạy ko

Phương pháp kinh nghiệm (Girgrah, 1977) cho phép tính trực tiếp E theo lượng chiếm nước thiết kế, M_tk:

$E = \frac{10M_{\text{tk}}}{120 + \sqrt{M_{\text{tk}}}}$

Tác động bất thường được tính đến bằng cách bổ sung hệ số tác động bất thường, có giá trị từ 1,3 với những tàu chở dầu hoặc hàng rời khô trong điều kiện thuận lợi nhất, và lên đến 3,0 với những tàu ro/ro hoặc phà trong điều kiện cập bến khó khăn.

Sự hấp thụ năng lượng của tấm chắn

Điều này cơ bản phụ thuộc vào diện tích tiếp xúc. Khi tiếp xúc nghiêng, diện tích này giảm nhỏ và có thể thu hẹp còn 0,25 m². Ngược lại, trong trường hợp tiếp xúc trực diện (thuận lợi nhất) thì diện tích tiếp xúc vẫn nhỏ hơn diện tích sườn bên ứng với chiều dài L của tàu.

Giữa sườn tàu và tấm chắn luôn có ma sát (trượt) với hệ số ma sát μ. Nếu tấm chắn bằng cao su thì hệ số ma sát với vỏ tàu thép là μ = 0,7. Hệ số này cần được giảm thiểu.

Ngoài ra, còn có thành phần lực theo phương thẳng đứng bởi sự nâng hạ mực nước và ma sát giữa vỏ tàu với tấm chắn. Lực này thường được trực tiếp ước tính qua lượng chuyển nước của tàu.

§18. Công trình bến

Hình 32. Bến kín (trái) và bến mở (phải)

Bến cảng được thi công bằng cách nạo vét một phần bùn cát trên bờ thoải (bến mở) hoặc nạo vét đồng thời tận dụng vật liệu để đắp bến (bến kín). Bến kín thường dùng trong trường hợp địa chất nền rắn chắc và độ sâu bến không lớn. Để đón được những tàu lớn, bến kín bằng tường cừ không đáp ứng được: người ta thường thay bằng bến nửa mở hoặc bến mở. Ngoài ra, bến mở với những trụ dài có thể xây dựng được trên bờ biển địa chất có lớp bùn dày.

Cao trình bến được thiết kế căn cứ vào:

• cao trình mặt sân bãi phía sau
• mực nước cao nhất quan trắc được và mực triều
• nước dâng do gió trong bể cảng
• tác động của sóng trong bể cảng
• loại tàu cập bến
• cơ sở hạ tầng, quy trình bốc dỡ hàng

Tải trọng lên bến gồm tải trọng theo phương đứng và tải trọng theo phương ngang. Tải trọng đứng gồm các tải trọng động, tải trọng do cần cẩu, v.v. Với bến mở tất cả tải trọng động được truyền theo cột hoặc lamella xuống nền đá. Tải trọng ngang có thể xuất hiện ở ba cao trình: tại mức ngang mặt bến, mức giữa mặt bến và đáy biển, và mức đáy biển (Hình 34). Để các nội lực không gây ra mô men có thể phá hoại công trình, trong bến mở cần lưu ý bố trí sao cho trụ kề bờ, mặt bến và neo đồng quy với nhau.

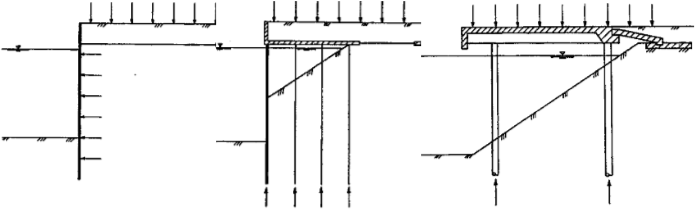
Hình 33. Tải trọng lên bến kín, bến nửa mở, và bến mở

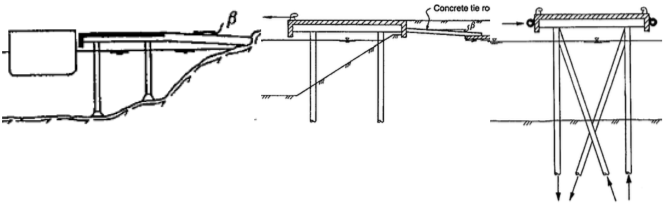
Hình 34. Bến mở và sự truyền tải trọng

Các nhân tố chi phối sự lựa chọn loại công trình bến:

• điều kiện địa chất
• việc thi công dưới nước
• kinh nghiệm thiết kế
• thiết bị thi công
• vật liệu
• thời gian thi công
• mở rộng bến trong tương lai
• khe giãn nở
• giá thành công trình

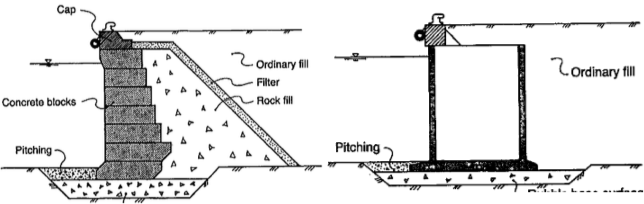
Hình 35. Dạng bến kín trọng lực: tường khối và caisson

Phương pháp tính toán thiết kế công trình bến, như dạng tường cừ chẳng hạn, là nội dung cơ bản của môn Cơ học đất / Nền móng. Để đơn giản hóa khâu tính toán, người ta lập nên những biểu đồ, như Hình 36, để tra trực tiếp ra chiều dài tối thiểu của tường cừ, mô men thiết kế, và lực neo. Dĩ nhiên những biểu đồ này chỉ áp dụng cho một số trường hợp cụ thể; còn trong trường hợp tổng quát ta cần phải giải bài toán phân tích lực bình thường.

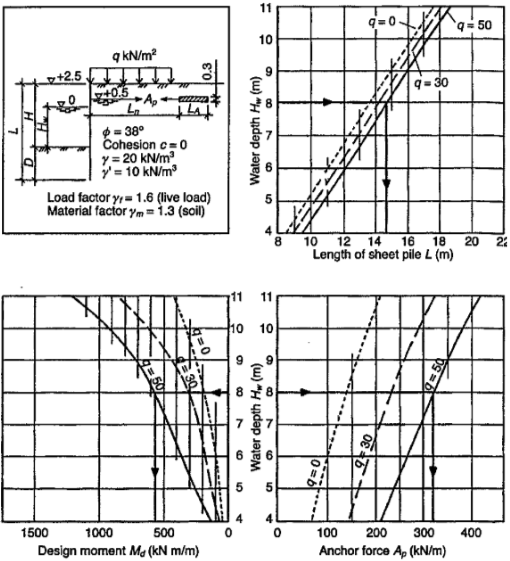
Hình 36. Biểu đồ tra tìm chiều dài cừ, mô men và lực neo (đều ở trục hoành) theo độ sâu nước (trục tung).

Tính toán ổn định bến mở bằng phương pháp ứng suất

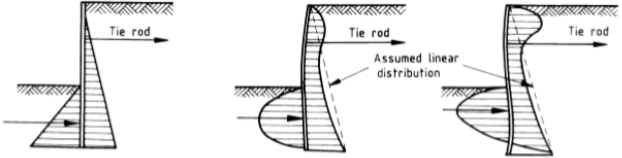
Hình 37. Phân bố ứng suất

Việc tính toán thiết kế cần được dựa trên một số giả thiết nhằm đơn giản hóa cấu trúc. Hình 37 cho thấy phân bố ứng suất trong ba trường hợp (từ trái qua phải): vách cứng chuyển vị ở chân (tựa đất tự do), vách đàn hồi chịu ứng suất đất ở hai mặt chủ động và bị động, và đàn hồi đâm sâu (tựa đất cố định). Trong khuôn khổ bài giảng, ta chọn trường hợp đơn giản (1).

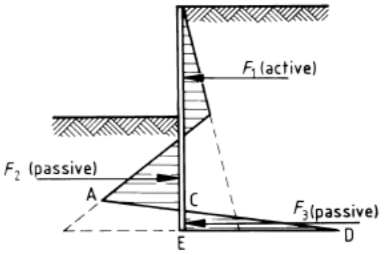
Hình 38. Cân bằng áp lực chủ động (active) - bị động (passive)

Theo cách tính cân bằng lực này (Hình 38), vách cừ phải đủ sâu để áp lực chủ động cân bằng với áp lực bị động. Giả sử rằng đất nền đồng nhất (có cùng chỉ tiêu cơ lý, cụ thể là dung trọng γ_S và có thể là lực dính C). Lưu ý rằng đất bão hòa nước nên ngoài ứng suất (σ) ta phải tính ứng suất hiệu dụng (σ′). Chọn gốc O ở mức cao trình mặt bến và trục z hướng xuống dưới, dọc theo tường cừ, quy trình để xác định các ứng suất phương ngang:

σ_ZZ = q_Z + ∑ γ dz
p = γ_W (z – z_W)
σ′_ZZ = σ_ZZ – p
σ′_XX = Kσ′_ZZ ± 2C √K , với K được chọn là K_cđ hoặc K_bđ tùy phía tường
$K_{cđ} = \frac{1 - \sin\phi}{1 + \sin\phi}$ và $K_{bđ} = \frac{1 + \sin\phi}{1 - \sin\phi}$
σ_XX = σ′_XX + p

Trường hợp có neo thì phải đưa lực căng neo vào phương trình cân bằng lực.

§19. Và tìm hiểu thêm …

Đến đây nội dung bài giảng đã hết. Dĩ nhiên nội dung của môn học còn rộng hơn nhiều. Để có được kinh nghiệm làm những dự án trong thực tế sau này, sinh viên cần trang bị Tiếng Anh thật tốt và tìm hiểu thêm thông tin từ những nguồn tài liệu sau đây.

Tập san khoa học. Tập san (hay tạp chí) khoa học là nguồn tài liệu quan trọng để cập nhật những kiến thức và công nghệ mới về chuyên ngành, nắm bắt xu hướng phát triển trên thế giới. Cũng như các ngành công nghệ khác nói chung, ngành kĩ thuật cảng chỉ cung cấp những tập san có độ ảnh hưởng (impact factor) tương đối khiêm tốn so với các ngành khoa học. Song kiến thức trong các tập san rất cô đọng, đạt chất lượng cao và bất cứ nghiên cứu phát triển (R&D) nào cũng cần tới. Một số tập san quốc tế về chuyên ngành bao gồm:

• Journal of Waterway, Port, Coastal, and Ocean Engineering của ASCE (Hiệp hội Hoa Kỳ về Kĩ thuật dân dụng), phát hành 6 số báo một năm.
• Journal of Navigation của ĐH Cambridge, 6 số báo một năm. Điều đáng lưu ý là năm 2015 tạp chí này có một bài báo về chủ đề tìm kiếm máy bay MH370 (mất tích năm 2014)!
• Journal of Korean Navigation and Port Research Mặc dù là nước mới phát triển so với Âu-Mỹ, song Hàn Quốc đã mạnh dạn xuất bản quốc tế những thành quả nghiên cứu của mình. Tạp chí này đã đạt độ ảnh hưởng 0,238 vào năm 2013.
• Một số tạp chí khác có liên quan đến những khía cạnh nhỏ của kĩ thuật cảng như: Ocean Engineering, Coastal Engineering, Coastal Engineering Journal, Applied Ocean Research, Proceedings of the ICE - Maritime Engineering.
• Hội thảo chuyên ngành. Đây là sự kiện được tổ chức để các nhà khoa học trình bày những ý tưởng mới và phác thảo các bài viết, trao đổi trực tiếp với các chuyên gia trước khi hình thành bài báo khoa học nghiêm chỉnh. ICCE (International Conference on Coastal Engineering) là hội thảo quan trọng nhất, được tổ chức 4 năm một lần. Các hội thảo khác về lĩnh vực biển hay kĩ thuật tài nguyên nước, chẳng hạn Coastal Structures, IAHR Congress đều nhiệt liệt chào mừng những báo cáo về chủ đề cảng và giao thông thủy.

Kỷ yếu của những hội thảo này là tập hợp những bài báo của các chuyên gia nhiều kinh nghiệm. Bảng 9 liệt kê một số bài báo trong kỷ yếu ICCE được dùng để làm chủ đề thảo luận trong một tiết học lớp 52B.

Bảng 9: Các chủ đề thảo luận lấy từ bài báo hội thảo ICCE 2012

Bài báo	Các vấn đề
Các công trình bến mở dưới tác dụng của luồng nước từ chân vịt tàu (T.giả: Yalcin Yuksel, Selahattin Kayhan, Yesim Celikoglu, Kubilay Cihan)	☑ khảo sát thực nghiệm những đặc tính dòng chảy ở đáy biển quanh chân cọc ☑ xác định ứng suất tiếp đáy biển và profin vận tốc gần các công trình bến mở ☑ giải thích sự xói lở trên mái dốc
Việc cải thiện khả năng tiếp cận đường thủy đến cảng Zeebrugge: nghiên cứu liên ngành (T.giả: Chantal Martens, Rosalia Delgado, Hadewych Verhaeghe, Toon Verwaest, Marc Willems)	☑ dòng chảy mạnh ở cửa vào cảng đang cản trở tàu tiến vào trong thời gian nước cao ☑ lớp bùn đáy dày cản trở giao thông trong cảng và đội giá thành nạo vét ☑ thiết lập tổng thể dự án, giải thích nghiên cứu mô hình số trị và vật lý
Mô phỏng máy tính cho chuyển động tàu đang neo chịu tác dụng của cộng hưởng trong vùng cảng mới Pohang (T.giả: Moonsu Kwak, Yongho Moon, Chongkun Pyun)	☑ phương pháp ước lượng chuyển động của tàu được neo & hiệu ứng của cộng hưởng cảng đối với chuyển động ☑ mô hình CGWAVE để tính sóng và hàm Green để mô tả chuyển động ☑ chuyển động tàu sẽ tăng 10%-30% so với trường hợp không cộng hưởng
Sự cơ động của bùn cát đáy khuấy lên bởi vệt tàu thủy ở Cảng Eagle, Washington, Hoa Kỳ (T.giả: David R. Michalsen, Zeki Demirbilek, Okey Nwogu)	☑ nghi ngờ sự xói mòn lớp bùn cát phủ tại đáy cảng ☑ mô hình sai phân hữu hạn 2D ghép với phương pháp panel Boussinesq để khảo sát ứng suất đáy của lớp phủ ☑ kết quả ứng suất vượt 100 Pa dọc theo tuyến tàu chạy

Sách chuyên khảo. Những cuốn sách chuyên khảo giúp ích cho nhiều lớp người đọc. Những người mới tìm hiểu chuyên ngành có thể đọc lấy kiến thức, còn những chuyên gia thì dùng sách như một tài liệu để tra cứu thông tin.

• Port Designer Handbook của Carl Thoresen là cuốn sách truyền đạt nhiều kinh nghiệm thực tế được viết bởi nhà kỹ sư tư vấn người Na Uy, và phản ánh được quy trình cơ bản về thiết kế cảng biển ở các nước Bắc Âu.

• Planning and Design of Ports and Marine Terminal (ấn bản lần 2) của Hans Agerschou và nnk có nội dung phong phú, đề cập đến nhiều khía cạnh thiết kế và vận hành cảng, và mới bổ sung một chương về MARPOL [Công ước quốc tế về chống xả thải từ trên tàu].

• Gregory Tsinker tập hợp một nhóm tác giả biên soạn cuốn sách Port Engineering: Planning, Construction, Maintenance, and Security chứa nhiều thông tin hữu ích về các vấn đề khác nhau của cảng biển.

• Yoshimi Goda (1935–2012) là nhà khoa học Nhật Bản nổi tiếng với những nghiên cứu về sóng ngẫu nhiên. Một số phương pháp và dữ liệu trong phần thiết kế công trình được lấy từ cuốn Random Waves and Design of Maritime Structures của ông.

• Gaythwaite với các cuốn sách Design of Marine Facilities for the Berthing, Mooring, and Repair of Vessels và Mooring of Ships to Piers and Wharves đã cung cấp thông tin về thiết kế bến bãi và khu neo đậu tàu, với những kinh nghiệm của chính tác giả.

Phụ lục

Tập giáo trình này được viết với cố gắng làm cho sinh viên càng dễ hiểu càng tốt. Bởi vậy, tên gọi và kí hiệu các đại lượng được thống nhất trong sách. Tên tiếng Anh giúp cho việc tra cứu tài liệu trên mạng, và khoảng giá trị điển hình (kèm theo đơn vị) giúp người đọc hiểu sâu hơn về bản chất vật lý các đại lượng được trình bày.

Tên gọi	Tiếng Anh	Kí hiệu	Khoảng giá trị
Bán kính cong tuyến luồng	Channel’s radius of curvature	Rcong	thường từ vài lần chiều dài tàu trở lên
Bán kính quán tính của tàu	Radius of inertia	Iq	(0,2 → 0,5) lần chiều dài tàu
Bề rộng tàu	Beam width	B	lên đến vài chục m
Bề rộng kênh / luồng	Channel width	W1, W2
Bề rộng dải điều động cơ bản	Width of basic maneuvering lane	WBM	(1,2 → 1,5) lần bề rộng tàu
Bề rộng dải vượt tàu	Width of passing lane	WP	tùy theo điều kiện giao thông, xác định theo quy phạm
Bề rộng dải lưu không sát bờ	Bank clearance width	WBg, W*Br	hai giá trị ứng với hai phía bờ tả, hữu
Bề rộng dự phòng tổng cộng		ΣWi	xác định theo nhiều tiêu chuẩn: sóng, gió, dòng chảy, độ sâu, mức độ nguy hiểm của hàng hóa, v.v.
Bề rộng đoạn kênh cong	Width of a curved channel	Wcong	tỉ số Wcong/B > 1, tra đồ thị
Chỉ số chiếm chỗ	Occupancy factor	ko	0 → 1
Chỉ số tắc nghẽn	Congestion factor	koʹ	0 → 1
Chiều cao sóng	Wave height	H	0 → 12 m (thường), có thể lớn hơn với sóng rogue
Chiều cao sóng ý nghĩa	Significant wave height	Hs, H1/3	khoảng 1,4×Hrms hay 1,6×H trong sóng ngẫu nhiên
Chiều cao sóng tới	Incident wave height	HI	< H0
Chiều dài sóng	Wave length	L	vài chục → < 200 m ở nước sâu, ngắn lại khi truyền vào gần bờ; vài trăm km với sóng triều ở ven bờ
Chiều dài tàu	Ship length	L	vài chục → khoảng 300 m. Thường cụ thể hóa thành các chiều dài LOA, LBP.
Chiều dài định hình	Length between perpendiculars	LBP, Lpp	LBP < LOA
Chiều dài tổng	Overall length	LOA
Chiều dài khúc thân song song	Parallel mid-body length	LPM	LPM ≈ 0,7LOA
Chu kì sóng	Wave period	T	1 s – 15 s với sóng gió; ½ ngày – 1 ngày với sóng triều
Chu kì đỉnh phổ	Spectral peak period	Tp	5 s → hơn 10 s; chỉ áp dụng với sóng gió; xác định từ phổ sóng bằng cách lấy nghịch đảo của giá trị f ứng với đỉnh của đồ thị phổ.
Độ chìm đều của tàu	Squat	SQUAT	thường < 1 m; nhưng càng tăng khi tàu chạy nhanh trong kênh hoặc luồng hẹp, nông.
Độ lưu không	Clearance depth	hC, hLK	1 vài mét; nếu nhỏ, tàu dễ mắc cạn
Độ sâu nước	Water depth	h	khoảng 10 mét trong bể cảng; sâu hơn ở trong luồng tàu
Động năng của tàu	Kinetic energy	*E *	nhiều kJ
Góc cập bến của tàu	Berthing angle	ϕ	thường từ 15° → 30°
Góc sóng tới	Incident wave angle	α	0° → 360° (so với phương pháp tuyến của đường bờ)
Góc phân phối năng lượng sóng		θ	–45° → +45° hoặc rộng hơn với sóng gió, hẹp hơn với sóng lừng; khoảng giá trị này đối xứng qua 0° (là góc ứng với hướng truyền sóng).
Hệ số béo	Blocking coefficient	CB	0,6 (tàu nhỏ) → 0,9 (tàu lớn)
Hệ số cản tiếp tuyến (do dòng chảy)		Ccản	Hệ số ma sát vỏ tàu, = 0,001 (tàu mới), = 0,004 (tàu đã qua sử dụng)
Hệ số cản dọc (do dòng chảy)		Cdọc	0,6 với mũi tàu cong
Hệ số cản ngang (do dòng chảy)		Cng	1 → ≈ 5,0 (tra biểu đồ Cng ~ h/D).
Hệ số (nhân tố) giam nước	Coefficient (factor) of water cushion	CC	0,6 → 1,0
Hệ số (nhân tố) khối lượng thêm	Coefficient (factor) of added mass	CH	>1, sơ bộ lấy bằng 1,5 với nước sâu và 1,8 với nước rất nông
Hệ số khúc xạ	Coefficient of refraction	Kr	nhỏ hơn và gần bằng 1
Hệ số (nhân tố) lệch tâm	Coefficient (factor) of eccentricity	CE	< 1, càng lớn khi tàu cập bến theo hướng càng song song với mặt bến
Hệ số nhiễu xạ	Coefficient of diffraction	Kd	0 → 1, càng nhỏ khi càng vào sâu trong vùng khuất sóng
Hệ số nước nông	Coefficient of shoaling	Ksh	≈ 1
Hệ số phản xạ	Coefficient of reflection	Cr	0 → 1; ≈ 1 với vách đứng, liền khối ; ≈ 0,5 với đập đá đổ có mái dốc khoảng từ 1:3 đến 1:2; và ≈ 0 với bãi biển thoải.
Hệ số (nhân tố) va chạm mềm	Coefficient of soft impact	CS	0,9 → 1,0
Khoảng cách từ điểm va chạm đến khối tâm		r	(0,25 → 0,35) chiều dài tàu
Số lượng bến	Number of berths	nb
Số tàu cập bến	Number of arrived ships	N
Số Froude (Frút)	Froude number	Fr, F	không thứ nguyên; đối với tàu, từ 0 → 0,7 do hiếm khi động cơ tàu đủ mạnh để vượt qua ngưỡng này
Số Reynolds (Rây-nôn)	Reynolds number	Re	không thứ nguyên, 0 → rất lớn
Tải trọng phân bố trên mặt bến	Distributed load on berth apron	q	T/m2 hoặc kN/m2
Tham số tập trung năng lượng theo hướng	Directional spreading parameter for wave spectra	s, smax	không thứ nguyên, = 10 với sóng gió và lên đến 75 với sóng lừng ở nước sâu; tăng dần khi vào vùng nước nông
Thể tích chiếm nước	Displacement	∇
Thông lượng hàng hóa	Throughput	Q	cỡ một vài trăm nghìn T/năm
Trọng số phân phối năng lượng theo hướng	Directional wave energy distribution parameter	D	0 → 1. D = hàm số của góc θ; song thường được cho dưới dạng tập giá trị tương ứng với một số hướng θ nhất định.
Vận tốc dòng chảy	Current velocity	V	hiếm khi vượt 1,0 m/s trừ những luồng triều mạnh
Vận tốc gió	Wind velocity	U	Có thể đo ở độ cao 10 m trên mặt biển
Vận tốc tàu	Ship velocity	VS	Trong điều động tàu, chậm: (2,5 → 4) m/s; trung bình: (4 → 6) m/s; nhanh: > 6 m/s.

---

1. SV có thể tạm thời truy cập trang web [http://coastal-study.uk:5100/] để trích xuất một đoạn số liệu WAVEWATCH-III với vị trí có kinh/vĩ độ chẵn nửa độ trên biển. ↩︎

2. Một ví dụ, xem tính toán ở trang web [http://nbviewer.jupyter.org/url/coastal-study.uk/webnotebooks/Diffraction Breakwater.ipynb] ↩︎