Mở đầu

Trong bài thực hành này, bạn sử dụng chương trình phần mềm Swan để tính truyền từ biển sâu vào gần bờ đảo. Khu vực được chọn là đảo Phú Quý (thuộc tỉnh Bình Thuận).

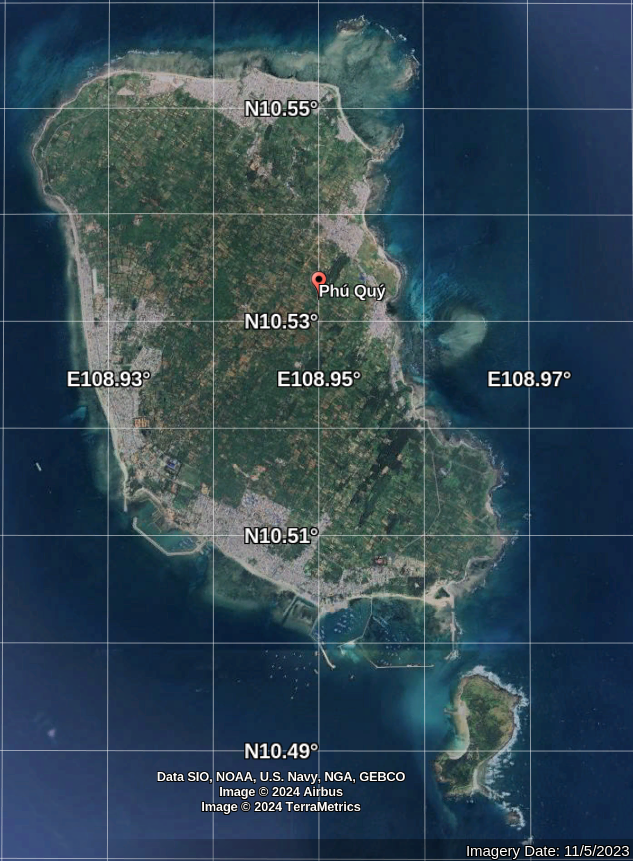
Hình 1

Phụ lục: Hướng dẫn sử dụng phần mềm

Sau khi tải file nén từ http://coastal-study.uk/Swan2D-Run.zip, bạn giải nén tất cả file vào cùng thư mục. Trên hệ điều hành Windows, thư mục này có một file chạy chương trình (LunoSwan.bat). Ngoài ra còn có các file thực thi (*.exe), file phụ trợ Swan (swanrun.bat), file mã lệnh (lunoswan2.lua), thư viện chương trình (*.dll); những file này đều quan trọng và phải được giữ nguyên, đầy đủ trong cùng thư mục. Hơn nữa, khi bạn chạy chương trình, bắt buộc phải có các file số liệu đầu vào (phuquy.bot, PhuQuy.dep) và file kết quả đầu ra. Những file này để cùng trong một thư mục, không nhất thiết phải là thư mục chương trình nêu nên, song bạn phải biết rõ tên và vị trí của thư mục này trong máy để có thể truy cập chúng dễ dàng.

Để cho tiện, trong đó cũng sẵn có file kịch bản tính truyền sóng cho đảo Phú Quý làm ví dụ (lunoswan2-phuquy.lua), kèm với các file kết qủa của lần chạy thử trước đó (*-PQ-.txt). Một số file bảng tính Excel được cung cấp thêm để phụ trợ cho việc biểu diễn số liệu địa hình và kết qủa tính toán.

Cám ơn sinh viên Nguyễn Văn Thuận (lớp 54B1) đã giúp biên tập số liệu địa hình, chạy thử kịch bản này và soạn các file Excel kết qủa.

Kích đúp file chạy LunoSwan.bat để chạy chương trình, cửa sổ lệnh bật ra. Sau khi chạy xong các file text kết qủa được tạo mới hoặc cập nhật.

Thao tác mã lệnh. Trước hết, chạy file scite-3.7.4x86.msi để cài đặt phần mềm SciTE nhằm thuận tiện biên soạn các file text số liệu.

Sau khi cài đặt xong, mở file lunoswan2-phuquy.lua để nhập các tham số tuỳ theo yêu cầu đề bài. (Click phải chuột -> Open with SciTE in a new tab. Sau đó chọn menu File - Enconding - UTF8 để hiện được chữ tiếng Việt. Chọn menu View - Line Numbers để hiện số dòng.) Lưu ý rằng chỉ nên sửa trong phạm vi đoạn mã lệnh quy định (đến dòng 205). Các câu lệnh có thể kiểu như:

• a1 = 4.15E-2 -- tham số a1 $\to$ chỉ sửa phần số;
• tenfile = 'diahinh.bot' -- file địa hình $\to$ chỉ sửa phần giữa hai dấu nháy;
• optOFFWCAP = true -- có chọn OFFWCAP không? $\to$ chỉ sửa true thành false hoặc giữ nguyên.

(Trong các câu lệnh trên, phần từ dấu -- trở đi là phần chú thích và không ảnh hưởng đến kết quả chạy mô hình. Đây là quy ước của ngôn ngữ lập trình Lua.)

Phần mềm chương trình này sẽ ghi ra một file có đuôi *.swn. Cấu trúc file này gồm nhiều câu lệnh khác nhau (Swan, 2016a). Khi chạy mô hình, file swan.exe được kích hoạt và đọc thông số từ file *.swn cùng một số file khác như địa hình (cũng được chỉ định từ file *.swn).

Cấu trúc file swn. Trong file này có: các câu lệnh, mỗi câu một dòng. (Riêng những câu lệnh dài quá thì sẽ có một dấu & trước khi xuống dòng.) Thứ tự các câu lệnh nói chung là quan trọng và phải tuân theo. Đứng đầu câu lệnh là các từ lệnh được quy định sẵn trong Swan. (Mỗi từ lệnh có thể viết gọn theo 4 chữ cái đầu tiên.) Sau từ lệnh là các số liệu (nếu là các chữ thì phải đặt trong 'dấu nháy'), hoặc các từ khoá. Từ lệnh và từ khoá thường được quy định viết chữ IN.

LunoSwan là chương trình tiện ích đơn giản; toàn bộ tính năng của Swan phức tạp hơn và bạn có thể tìm hiểu để nhập thêm các giá trị từ khoá, hoặc tự sửa file *.swn trước khi chạy mô hình, tuỳ theo nhu cầu.

Phổ sóng

Phổ sóng nói nôm na là sự phân bố của mật độ năng lượng sóng theo các “phân khúc” tần số $f$ ($\Rightarrow$ chu kì). Cũng cần nói thêm, phổ sóng còn thể hiện sự phân bố theo các “phân khúc” hướng ($\theta$) trải sang hai phía của hướng truyền sóng chính. Sóng càng đều (như sóng lừng), phổ sóng càng hẹp (Hình 2).

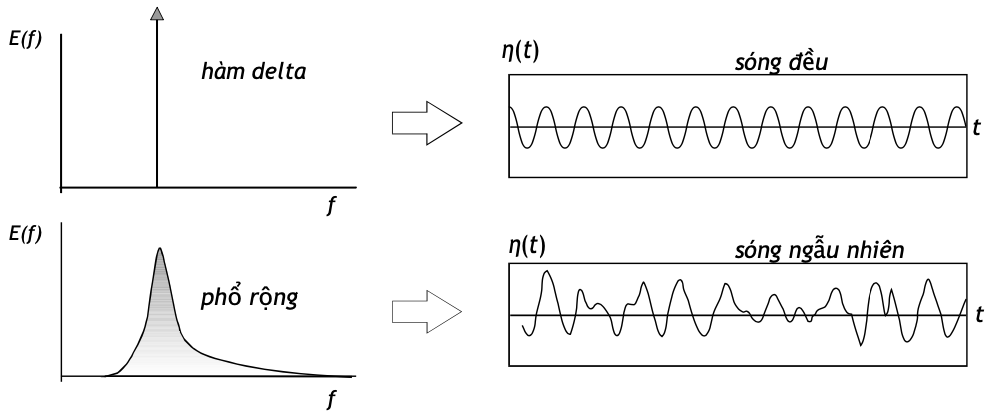
Hình 2

Trong thực tế, hình dạng của phổ sóng được quy về một số loại chuẩn, như Pierson-Moskowitch (PM), JONSWAP, hay TMA (Texel-Marsen-Arsloe). Có thể tham khảo sách của Nguyễn Mạnh Hùng và Nguyễn Thọ Sáo (2005) (http://coastal-study.uk/Pho_song_ven_bo.pdf).

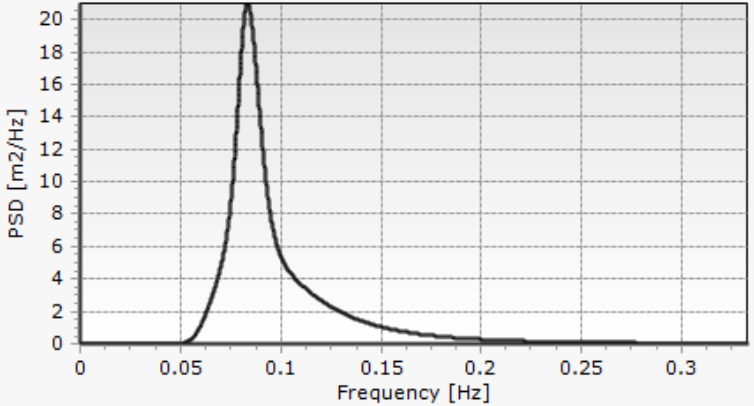
Hình 3

Ví dụ: Cho một phổ sóng trên hình 3. Có thể nhận diện loại phổ (PM, JONSWAP, hay TMA) và tính ra chiều cao sóng ý nghĩa cũng như chu kì sóng đỉnh phổ.

Lý thuyết mô hình sóng phổ

Trong mô hình sóng phổ như Swan, máy thực hiện tính toán để giải phương trình, tìm ra phân bố của mật độ năng lượng phổ trong không gian và theo thời gian. Riêng trong bài toán ổn định (điều kiện sóng ngoài khơi không có diễn biến đáng kể), thì bài toán chỉ thu về tính phân bố trong không gian.

Phương trình cơ bản của Swan là phương trình cân bằng mật độ “hoạt độ” sóng $N$ (wave action density). Lý do chọn hoạt độ sóng thay vì mật độ năng lượng sóng ($E$) là vì cách thứ nhất cho phép giải bài toán tổng quát khi có mặt dòng chảy. $\frac{\partial N}{\partial t} + c_{g,x} \frac{\partial N}{\partial x} + c_{g,y} \frac{\partial N}{\partial y} + c_{g,\theta} \frac{\partial N}{\partial \theta} + c_{g,\sigma} \frac{\partial N}{\partial \sigma} = \frac{S}{\sigma} \qquad \qquad (1)$

trong đó $N$ và $E$ đều là các hàm của $x$, $y$, $\theta$, $\sigma$.

Từ việc xác định phổ năng lượng sóng có thể dễ dàng suy diễn ra các đặc trưng sóng là chiều cao và chu kì sóng, để phục vụ bài toán kĩ thuật; Swan đã tính điều này và cho phép xuất kết quả $H_s$, $T_p$, v.v.

Trong mô hình Swan, một loạt các yếu tố làm tăng cường hoặc tiêu tán sóng trong quá trình truyền đi đã được xét đến: (Swan, 2016b)

• Tác động bởi gió, làm tăng cường sóng.
• Thành phần tiêu tán năng lượng là tổng hợp của ba yếu tố: sóng bạc đầu, ma sát đáy và sóng vỡ do nước nông.
• Tương tác giữa các sóng phi tuyến.

Từng thành phần nêu trên được quy định bằng những tham số nhất định trong mô hình Swan (Mục “tham số”).

Những cơ chế biến đổi

Trong phương trình (1), thành phần nguồn $S$ được biểu diễn bằng tổng các thành phần: $S = S_{g} + S_{wc} + S_{f} + S_{br} + S_{nl}$.

Sự phát triển của sóng do gió được đặc trưng bởi một số hạng nguồn $S_{g}$. Số hạng này trực tiếp phụ thuộc vào năng lượng $E$ theo hệ thức $S_{g} = A + BE(\sigma, \theta)$ trong đó $A$ và $B$ phụ thuộc vào chu kì sóng cùng tốc độ và hướng gió. Với hướng phổ $\theta$ không lệch quá hướng gió $\theta_{gio} \pm 90^\circ$ thì:

$A = \frac{1,5 \times 10^{-3}}{g^2 2\pi } [u_* \cos(\theta - \theta_{gio})]^4 \exp[-(\sigma / \sigma_{PM}^*)^{-4}] \qquad \qquad (2)$

(Còn nếu hướng phổ lệch quá $\pm 90^\circ$ so với hướng gió thì $A = 0$.)

ở đây $\sigma_{PM}^* = 2\pi \displaystyle{\frac{0,13g}{28u_*}}$ là tần số đỉnh trong phổ PM, $u_*$ là vận tốc ma sát của gió, được liên hệ với $U_{10}$, tốc độ gió 10 m trên mặt biển, thông qua hệ số ma sát gió $C_D$:

$C_D =\left\lbrace \begin{array}{ll} 1,2875 \times 10^{-3} & \text{với } U_{10} < 7,5 \text{ m/s}; \\ (0,8 + 0,065U_{10}) \times 10^{-3} & \text{với } U_{10} \ge 7,5 \text{ m/s}; \end{array} \right. \qquad \qquad (3)$

Hệ số luỹ tiến tăng trưởng sóng, $B$, có thể được xác định theo:

$B = 0,25 \frac{\rho_{nước}}{\rho_{khí}} \left[ 28 \frac{u_*}{c} \cos(\theta - \theta_{gió}) - 1 \right] \sigma \qquad \qquad (4)$

(Nếu tính ra kết quả âm thì lấy $B = 0$.)

Sóng bạc đầu (white-capping) $S_{wc}$ là thành phần làm tiêu tán năng lượng sóng; theo Hasselman (1974):

$S_{wc} = -C_{wc} \left( (1 - n) + n \frac{k}{\tilde{k}} \right) \left( \frac{\tilde{s}}{\tilde{s}_{PM}} \right)^p \frac{\tilde{\sigma}}{\tilde{k}} k E(\sigma, \theta) \qquad \qquad (5)$

trong đó độ dốc sóng trung bình $\tilde{s}$ được định nghĩa bởi $\tilde{s} = \tilde{k} \sqrt{m_0}$ còn $\tilde{s}_{PM}$ là độ dốc sóng trung bình trong phổ Pierson-Moskowitz, $\tilde{s}_{PM} = \sqrt{3,02\times 10^{-3}}$. Các trị số $C_{wc}$, $n$ và $p$ đều là các thông số điều chỉnh được. Gợi ý lựa chọn: $n = 0$, $C_{wc} = 2,36 \times 10^{-5}$ và $p = 4$.

Ma sát đáy $S_{b}$ gây tiêu tán năng lượng được biểu diễn qua đại lượng:

$S_{b} = -\frac{C_{b}}{g} \left[ \frac{\sigma} {\sinh (kh)} \right]^2 E(\sigma, \theta) u_{rms, b} \qquad \qquad (6)$

trong đó $u_{rms, b}$ là căn quân phương vận tốc quỹ đạo sát đáy, còn hệ số ma sát đáy, $C_b$ được tính theo một trong ba cách:

• mô hình thực nghiệm JONSWAP (chú ý: đây không phải là một phổ sóng) của Hasselman và nnk. (1973), theo đó $C_{b} = 0,038 / u_{rms, b}$ với sóng lừng và $0,067 / u_{rms, b}$ với sóng gió.
• mô hình định luật cản của Collins (1972), $C_b = 0,015$
• mô hình nhớt rối của Madsen và nnk. (1988), $C_b = f_w / \sqrt{2}$; hệ số ma sát phi thứ nguyên trong chế độ chảy thành nhám thuỷ lực lấy bằng $f_w = 0,30$.

Mô phỏng sóng vỡ (breaking) do nước nông $S_{ds,br}$ được thiết lập theo công thức của Battjes và Janssen (1978):

$S_{b} \approx -\frac{1}{4} Q_b H_{max}^2 / \overline{T_0} \qquad \qquad (7)$

trong đó $\overline{T_0}$ là chu kì sóng trung bình xác định theo cách “giao cắt qua 0”, $H_{max}$ là chiều cao sóng lớn nhất (bị vỡ) $H_{max} = \gamma (h + \eta)$, và hệ số sóng vỡ $\gamma$ là thông số điều chỉnh được, nhận giá trị mặc định bằng 0,73. Dĩ nhiên, không phải mọi con sóng đều vỡ do đó cần phải nhân với “tỉ lệ xuất hiện sóng vỡ”, $Q_b$ xác định qua hệ thức: $(1 - Q_b) / Q_b = - (H_{rms}/H_{max})^2$.

Tương tác giữa các sóng phi tuyến có hai loại: tương tác sóng quadruplet rất quan trọng ở vùng nước sâu và tương tác sóng triad ở vùng nước nông. Cả hai thành phần này đều rất khó xác định chính xác; người ta đã áp dụng các phương pháp tính xấp xỉ như DIA, LTA trong Swan. Các biểu thức toán học liên quan rất phức tạp do đó sẽ không được trình bày ở đây.

Để giải được phương trình (1) nhằm tính ra biến hình phổ sóng, cần triển khai các phương pháp số phức tạp.

Ảnh hưởng của đại lượng nguồn đến biến hình phổ sóng

Rõ ràng các số hạng nguồn ảnh hưởng đến phổ sóng: tăng năng lượng sóng đồng nghĩa với tăng diện tích dưới đường cong phổ. Nhưng sự tăng năng lượng này không trải đều toàn dải phổ mà tập trung vào những khoảng tần số nhất định. Như trên Hình 4, các nguồn bổ sung năng lượng được biểu thị bằng mũi tên trắng, nguồn rút năng lượng: mũi tên đen, chuyển năng lượng: mũi tên xám, và biến hình phổ: mũi tên nét mảnh. Điều này sẽ được kiểm chứng khi chạy mô hình.

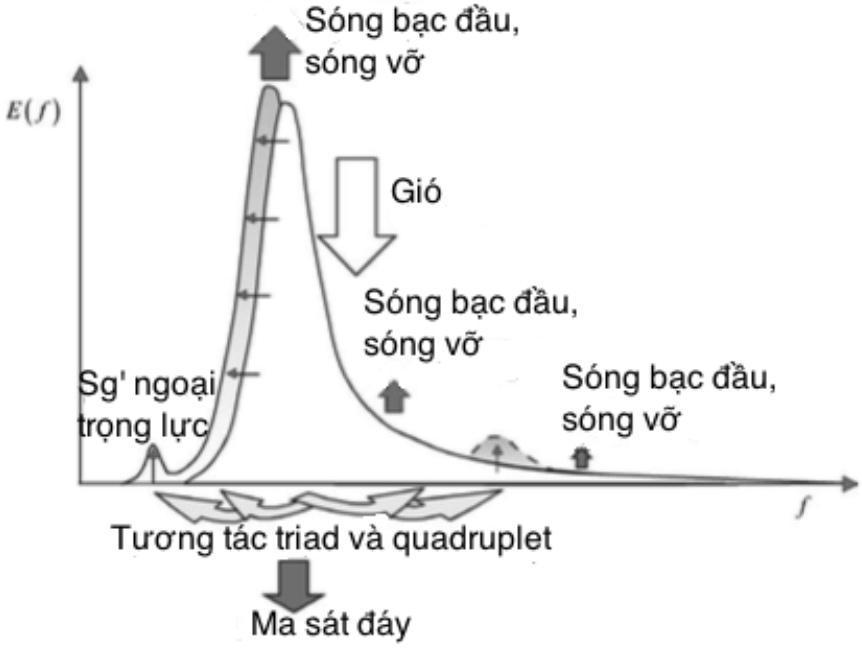
Hình 4

Các mã hiệu quy ước

Có một số biến số đóng vai trò mã hiệu quy ước trong chương trình Swan. Đây không phải các tham số quan trọng; nhưng cần kiểm tra trước khi chạy chương trình.

Hướng. Góc hướng được xác định theo một trong hai quy ước:

• Nautical là hướng địa lý, thường dùng để biểu diễn hướng gió: ví dụ gió Bắc thì góc bằng 0°, gió Đông ứng với góc 90°, gió Đông Nam: 135°.
• Cartesian là hướng toạ độ Đề các (hay góc quay của vectơ quanh gốc toạ độ), thường dùng để biểu diễn hướng dòng chảy: ví dụ từ Bắc (đến Nam) thì góc bằng 270°, từ Đông (sang Tây): 180°, từ Đông Nam (lên Tây Bắc): 135°. Trong hệ toạ độ Đề các, với trục x thì chiều âm sẽ có hướng tây (W) còn chiều dương có hướng đông (E).

Số liệu địa hình đáy

Swan cần số liệu địa hình đáy, nghĩa là ma trận độ sâu hay cao trình đáy. Ở ví dụ này ta có số liệu cao trình (z). Các điểm số liệu này ở trên lưới chữ nhật có khoảng cách đều theo cả phương Tây-Đông lẫn Nam-Bắc (Δx = Δy = 30 m). Số liệu gốc ở Sheet1 file Hieu chinh dia hinh phu quy.xlsx. Do số liệu này chưa hợp lý, phía Đông của đảo vẫn có chỗ đất cao, ví dụ ô HK256 có gía trị 12 trong khi đáng ra vị trí đó phải là nước. Số liệu được điều chỉnh lại ở sheet sua dh (2). Số liệu chỉnh này được copy và đưa vào file phuquy.bot.

✍ Định khoảng cách giữa các điểm tính (dxinp, dyinp trên dòng INPGRID BOT), kiểm tra số lượng các điểm địa hình (mxinp, myinp) và toạ độ điểm dưới phía trái của miền (xpinp, ypinp). Tọa độ được xác định trên bản đồ (Google Earth).

Theo quy ước về độ sâu: mặc định là càng sâu, địa hình đáy càng dương. Tuy nhiên, ở đây số liệu địa hình được nhập dưới dạng cao trình, bởi vậy cần kiểm tra hệ số điều chỉnh bằng -1 trong lệnh READINP BOT (dòng 226 file lunoswan2-phuquy.lua). Còn file .bot được bố trí theo hàng cột giống như thể hiện địa lý (hướng x, y).

Miền tính toán

Miền tính toán tạm lấy bằng phạm vi số liệu (thực tế có thể lấy nhỏ hơn). Trong trường hợp này, để dễ theo dõi kết qủa, ở ví dụ mẫu thì miền tính toán chỉ gồm 60×90 ô lưới.

✍ Hãy kiểm tra chiều dài miền tính toán và khoảng cách giữa các điểm tính (thuật ngữ gọi là bề rộng ô lưới). Lưu ý: Các điểm tính toán phải đủ dày mới chính xác (có thể dày hơn số điểm địa hình); tất nhiên khi đó chương trình sẽ chạy lâu hơn. Nhập số liệu vào chương trình và kiểm tra mục CGRID.

Đặc điểm hơi khó trong mô hình sóng đó là ngoài chiều không gian còn có “chiều phổ”. Như vậy tại mỗi điểm lưới (x, y), có hai chiều phổ. Tại mỗi điểm có một “quả núi” mật độ năng lượng mà người ta thường biểu diễn dưới dạng đường đồng mức. Trong hình này, số múi hướng, các giới hạn tần thấp ($f_{low}$), tần cao ($f_{high}$), số khoảng tần được chỉ định. Các dải tần sẽ dãn cách theo thang logarit, cho bởi hệ thức: Số khoảng tần = $\ln(f_{high}/f_{low}) / \ln(1,1)$.

Số liệu sóng

Điều kiện sóng trong tự nhiên luôn biến đổi trong không gian và theo thời gian. Để đơn giản, trong mô hình ta sẽ tính với một số điều kiện sóng “điển hình”. Ta đã biết để đặc trưng cho sóng ngẫu nhiên có hai thuộc tính là chiều cao sóng ý nghĩa và chu kì sóng đỉnh phổ. Trong bài toán truyền sóng, điều kiện biên phía biển đóng vai trò quyết định động thái sóng trong vùng. Biên này gồm hai yếu tố:

• Hình dạng phổ sóng: cho phép lựa chọn giữa JONSWAP và PM. Với mỗi cách, cần chỉ định xem: chu kì chỉ định là $T_p$ hay $T_m$, và độ phân tán hướng lấy theo số mũ (POWER) hay theo độ (DEGREE). Riêng phổ JONSWAP, giá trị mặc định của thông số γ = 3.3.
• Phạm vi không gian, thời gian của biên: biên được đặt ở phía nào (N, S, E, W)? Chỉ định giá trị của các đặc trưng sóng, gồm $H_s$, $T_p$, φ (hướng sóng) và độ phân tán hướng (dd). Các thông số này có thể là không đổi (một bộ giá trị duy nhất), hay biến đổi theo thời gian. Trong ví dụ này, ta chỉ xét các thông số sóng không đổi.

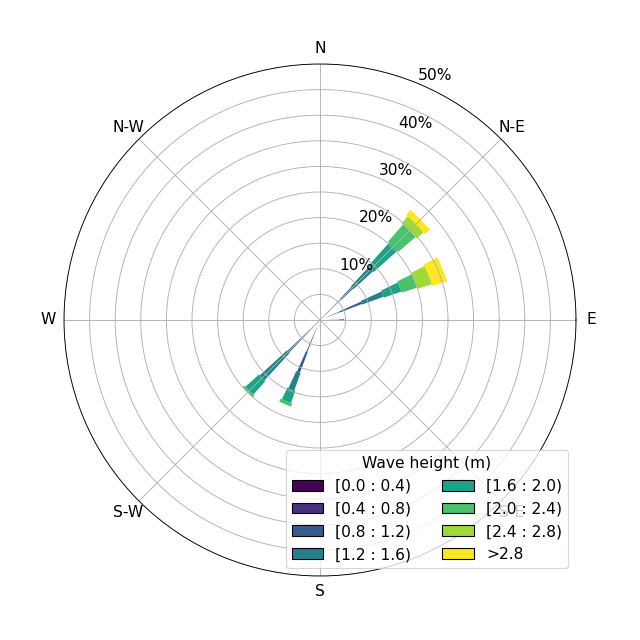
Hình 5

✍ Với ví dụ sóng như ở hoa sóng hình 5 (được tạo từ file Excel so lieu song phu quy.xslx), hãy xác định các đường biên của miền có sóng đi vào. Sửa lại thông tin tương ứng trong file số liệu (mục BOUND). Chọn loại phổ phù hợp cho điều kiện biên và nhập các đặc trưng sóng.

Điều kiện ban đầu

Số liệu sóng trong Mục “Sóng” đóng vai trò điều kiện biên (phía biển) của mô hình. Còn điều kiện ban đầu của mô hình, mặc dù không quan trọng bằng, song vẫn cần khai báo.

Điều kiện gió

Gió là nhân tố ảnh hưởng quy định sự phát triển sóng. Gió được coi là:

• phân bố đều trên miền tính toán và không đổi theo thời gian. Các tham số đưa vào là tốc độ gió, hướng gió (theo quy định Nautical) (gió ở độ cao 10 m), hoặc
• phân bố không đều trên miền tính toán: Swan cho phép trường hợp này, nhưng để đơn giản ta sẽ không dùng trong bài tập.

✍ Hãy nhập tham số gió thích hợp theo điều kiện khí hậu của khu vực nghiên cứu; ví dụ gió mùa đông bắc, tốc độ gió 8.0 m/s.

Mực nước

Mực nước là yếu tố quan trọng, làm ảnh hưởng đến độ sâu nước, và do đó đến hiện tượng sóng vỡ. Quy định mực nước = 0 là ngang với mức số không trong số liệu địa hình. Khi đó, có hai cách khai báo mực nước như sau:

• Mực nước không đổi. Chỉ định giá trị mực nước ngay sau từ khoá SET.
• Mực nước biến đổi; khai báo theo tinh thần tương tự địa hình ở mục “Số liệu địa hình”, máy sẽ tự nội suy (theo cách giống như với địa hình đáy). Chú ý kiểm tra dòng lệnh INPGRID WLEV.

Chọn các tham số cho mô hình

Các tham số cũng là đầu vào của chương trình tính, nhưng khác với các số liệu (như địa hình và sóng), tham số không đa dạng bằng, và có thể chọn một giá trị điển hình trong khoảng giá trị thường gặp trên thực tế. Chẳng hạn, tham số khối lượng riêng của nước biển điển hình vào khoảng 1025 kg/m³, dù rằng giá trị này vẫn có thay đổi theo nhiệt độ và độ muối. Độ nhớt của nước biển phụ thuộc mạnh vào nhiệt độ và có lẽ lớn hơn giá trị mặc định 1.0E-6 $=1\times 10^{-6}$ m²/s. Trong chương trình, các tham số này được nhập trực tiếp trên cửa sổ giao diện; nhiều tham số mô hình quy định độ lớn của các đại lượng (số hạng) nguồn gây biến hình phổ sóng.

Tạo sóng

Tương ứng với số hạng nguồn $S_g$, ta cần khai báo cơ chế tạo sóng. Chế độ mặc định là Swan chạy chế độ “thế hệ 3” (GEN3) đối với tạo sóng, tương tác phi tuyến quadruplet và bạc đầu. Công thức của Komen được dùng mặc định. Hệ số tiêu tán sóng bạc đầu $C_{ds}$ và độ dốc sóng $\tilde{s}_{PM}^2$. Một phương án khác là công thức Janssen, trong đó có hai hệ số: một hệ số khác quy định năng lượng bạc đầu tiêu tán, $C_{ds} / \tilde{s}_{PM}^4$ và hệ số δ quy định sự phụ thuộc hiện tượng bạc đầu theo số sóng. Các giá trị mặc định: cds2 = 2.36E-5, stpm = 3.02E-3, cds1 = 4.5, delta = 0.5.

Cả hai phương án đều có tùy chọn số hạng tuyến tính A (như phương trình (2)); mặc định a = 0.0015.

✍ Hãy nhập các giá trị tham số phù hợp.

Ma sát đáy

Ma sát đáy, có vai trò tiêu tán năng lượng sóng, được tính theo 1 trong 4 cách. Ba cách đã được trình bày sau PT (6). Còn một cách nữa là tính ma sát trực tiếp từ đường kính hạt cát (Smith, 2011).

Đường kính hạt bùn cát, $D$, tốt nhất nên lấy từ biểu đồ cấp phối hạt của mẫu bùn cát đáy biển ven bờ vùng dự án. Độ nhám đáy biển $k_s$ có lẽ là thông số khó xác định đúng nhất, và được chọn theo công thức sơ bộ: $k_s = 2,5 D$. Kết hợp với đặc trưng thủy động lực $A_b$ (biên độ dao động phần tử nước sát đáy), công thức Swart cho ta giá trị của hệ số ma sát: $f_w = \exp [ 5,213 (k_s / A_b)^{0,194} - 5,977 ]$

✍ Hãy ước tính giá trị của hệ số ma sát $f_w$ tính theo đường kính hạt và so sánh với các hệ số ma sát Madsen.

Sóng vỡ

Hệ số sóng vỡ (γ) có thể chọn là một hằng số (khi đó dùng từ khoá BREAK CONST); kèm theo một hệ số alpha đặc trưng cho tốc độ tiêu tán năng lượng (giá trị mặc định là 1,0).

Hệ số sóng vỡ cũng có thể được tính theo phương pháp đáy dốc - chiều sâu (BKD). Khi đó ngoài alpha, phải nhập thêm $\gamma_0$ và a1, a2, a3 (các giá trị mặc định lần lượt là 0.54, 7.59, –8.06, 8.09).

Các tham số nâng cao

Trong chương trình LunoSwan cho phép ta nhập những thông số nâng cao, theo nghĩa là không có sẵn trong giao diện; việc nhập tiến hành thông qua mục riêng. Bạn có thể tự gõ tên từ khoá và giá trị. Các cơ chế biến đổi sóng “nâng cao” thường gặp là: thực vật (VEGE), rối động (TURB) và bùn (MUD).

Kiểm tra số liệu và chạy chương trình

Các số liệu sau khi được nhập hết trong file lunoswan2-phuquy.lua, cần được kiểm tra một lượt. Lưu ý xem phần mã lệnh xem có gì bất thường không:

• Các từ khóa được viết chữ in;
• Các số được viết rõ ràng, tách rời nhau;
• Mỗi giá trị được chỉ định sẽ tương ứng với 1 con số trong dòng lệnh của file .swn.
• Có đủ các dòng lệnh bắt buộc như TEST, COMPUTE và STOP.

✍ Hãy lý giải giá trị các thông số được chọn (mục “Tham số”).

Khi kiểm tra xong số liệu, lưu file số liệu rồi chạy chương trình (LunoSwan.bat) và quan sát kết quả in ra trong ô bên cạnh xem có lỗi không.

Trong ví dụ này, mô phỏng được thực hiện ở chế độ “tĩnh tại”, nghĩa là sóng sẽ dần phát triển đến khi trạng thái sóng mặt biển ổn định và không thay đổi theo thời gian nữa; khi đó ngừng tính toán và báo cáo kết quả. Để tính toán phương trình vi phân ổn định, từ điều kiện ban đầu, máy sẽ thực hiện tính lặp nhiều lần đến khi kết quả giữa các lần lặp không thay đổi.

Lý giải kết quả

Trong mô hình Swan, có các kết quả đầu ra mô hình như sau:

• Phân bố trường các đại lượng (mã hiệu như sau: XP, YP: toạ độ của điểm kết quả, HSIGN: chiều cao sóng ý nghĩa, DIR: hướng sóng, PER: chu kì sóng, DEPTH: độ sâu nước, WATLEV: mực nước, WLEN: chiều dài sóng trung bình, SETUP: độ dềnh nước do sóng, GENWIND: tốc độ sinh năng lượng do gió, DISSIP: tốc độ tiêu tán năng lượng tổng cộng, DISBOT: tốc độ tiêu tán năng lượng do ma sát đáy, DISSURF … do sóng vỡ, DISWCAP … do sóng bạc đầu). Lưu ý tất cả năng lượng đang có đơn vị m$^2$/s, cần nhân với giá trị $\rho g$ = 9810 $\mathrm{kg m}^{-1} \mathrm{s}^{-2}$ để được đơn vị thực thụ là W/m$^2$.

• Phổ sóng. Thông tin phổ sóng được trình bày theo một trong hai dạng: phổ 1 chiều (SPEC1DorSPEC2D = ’SPEC1D’) hoặc 2 chiều (… ’SPEC2D’). Với hai dạng này, file kết quả sẽ có phần chung đều là các vạch chia tần số trong phổ sóng (AFREQ).

  1. Đối với phổ 1D, số liệu phổ bao gồm ba số trên một dòng: tung độ phổ (tức mật độ năng lượng), hướng năng lượng chính, và độ tản hướng (thể hiện phân phối năng lượng).
  2. Đối với phổ 2D, số liệu bao gồm các vạch chia hướng trong phổ (CDIR) và bảng số phân bố hai chiều. Bảng này cần được lấy giá trị để nhân với hệ số FACTOR.

Tìm kết quả được xuất ra ở các file có tên giống như đã quy định ở các dòng 9–10 của file đầu vào. File block là trường các yếu tố, table chứa biến thiên yếu tố tại một vị trí hoặc một tuyến, còn spec là phổ sóng tại các vị trí chọn trước.

Riêng trong file trường (block), mỗi gía trị chiếm 4 kí tự (kể cả dấu chấm phân cách); ở ô không có gía trị thì sẽ có 4 dấu sao liền nhau (****). Có thể đưa kết qủa vào bảng tính, như trong file ket qua SWAN.xls, sheet HSIG (đơn vị cm). Để trực quan, có thể hiển thị theo cách “tô màu”: trong bảng tính chọn vùng chữ nhật có số liệu, sau đó chọn menu Conditional Formatting $\to$ Color Scale. Màu sắc được tô vào các ô kiểu như trong file bảng địa hình ta đã xem.

Với các kết qủa tại điểm và tuyến (nếu có) thì có thể vẽ đồ thị dạng đường được.

✍ Nhận xét kết quả theo một số ý sau:

• Sự giảm chiều cao sóng từ phía biển về bờ;
• Sự khác biệt giữa hình dạng phổ sóng ở hai vị trí: xa bờ (nước sâu), và gần bờ (nước nông). Riêng với phổ sóng 2 chiều, cũng có thể hiển thị kiểu tô màu như đã làm với Hs.

✍ Phân tích độ nhạy. Kết quả tính toán phụ thuộc một cách phức tạp vào nhiều đại lượng (hay thông số) khác nhau. Để đánh giá ảnh hưởng của đại lượng đến kết quả ta cần phần tích độ nhạy: giữ nguyên từng thông số rồi thay đổi các thông số còn lại và quan sát sự thay đổi kết quả. Trong bài này, bạn hãy chọn lấy một tham số; thay đổi tham số này theo mức nhất định, ví dụ đường kính hạt $\pm 10\%$ hay mực nước $\pm$ 10 cm. Lưu file thành các kịch bản riêng, trong đó đặt tên file kết quả khác nhau. Lần lượt chạy chương trình cho từng kịch bản rồi so sánh kết quả trong các file.

Bộ môn Công trình Biển và Đường thuỷ, Khoa Công trình, trường ĐH thủy lợi, cập nhật 10/2024. Bản gốc tháng 2/2018.